محاسبه مقاومت برشی حاصل از آرماتورهای عرضی

محاسبه مقاومت برشی حاصل از آرماتورهای عرضی

با توجه به مفاهیم مطرح شده در قسمت اول فصل، فولادهای عرضی به شکل های مختلفی می توانند در مقطع به کار برده شوند. نحوه قرارگیری آرماتورهای عرضی در مقطع و راستای آنها، یکی از مهمترین عوامل تعیین کننده در مقاومت برشی آرماتورهای عرضی محسوب می شود.

به طور کلی آرماتورهای عرضی در چهار گروه اصلی طبقه بندی می شوند که در ادامه به شرح نوع قرارگیری و نحوه محاسبه مقاومت برشی تامین شده توسط آنها می پردازیم.

1-فولادهای عرضی عمود بر محور طولی عضو

این حالت یکی از متداول ترین و مناسب ترین حالات به کارگیری آرماتورهای عرضی محسوب می شود. در این حالت برای محاسبه مقاومت آرماتورهای عرضی، از رابطه زیر استفاده می شود:

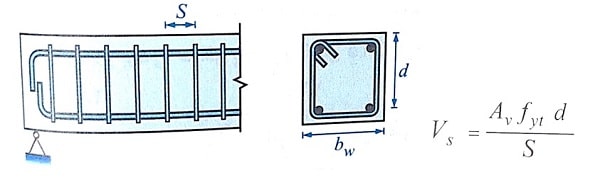
V_s: مقاومت برشی اسمی آرماتورهای عرضی، نیوتن.

A_v: مجموع مساحت شاخه های آرماتور عرضی عمود بر محور طولی عضو، میلی متر مربع.

F_yt: مقاومت تسلیم مشخصه فولادهای عرضی، مگاپاسکال.

S: فاصله طولی بین آرماتورهای عرضی، میلی متر.

با توجه به شکل مقطع و نوع المان، آرماتورهای عرضی عمود بر محور طولی عضو می توانند به صورت هر یک از موارد زیر مورد استفاده قرار بگیرند.

الف)خاموت، تنگ و یا دورگیرهای متعامد.

ب)شبکه های سیمی جوش شده به صورت متعامد بر محور طولی عضو.

ج)دورپیچ که در خصوص ستون ها و شمع های با مقطع دایره کاربرد دارد.

نحوه محاسبه A_v در مقاطع

1)در بسیاری از مقاطع بتن آرمه، به خصوص در ستون ها، علاوه بر یک خاموت بسته، از آرماتورهای عرضی سنجاقی یا رکابی نیز استفاده می شود.این آرماتورها عمدتا به منظور مهار میلگردهای طولی و همچنین افزایش مقاومت برشی آرماتورهای عرضی در مقطع به کار برده می شوند. نکته مهمی که باید به آن توجه نمود این است که در محاسبه A_v، باید سطح مقطع تمام شاخه های عرضی که در راستایی موازی نیروی برشی وارد بر مقطع به کار برده شده اند را با هم جمع کرد. در این خصوص به نحوه محاسبه A_v در مقاطع زیر دقت کنید:

2)در مقاطعی که در آنها از تنگ مدور یا دورپیچ به عنوان آرماتور عرضی استفاده می شود، سطح مقطع A_v که در محاسبه V_s به کار برده می شود، دو برابر مساحت میلگرد تنگ یا دورپیچ می باشد.

فولادهای عرضی مورب نسبت به محوری طولی عضو

در این حالت آرماتورهای عرضی (خاموت ها) به صورت مورب و با زاویه حداقل 45 درجه نسبت به محور طولی عضو به کار رفته اند. توجه شود در این حالت در نمای مقطع در شکل زیر، در هر گام دو شاخه از خاموت عرضی وجود خواهد داشت.

آلفا: زاویه مورب بین آرماتورهای عرضی و محور طولی عضو.

سایر پارامترها مطابق مورد 1 تعریف می شوند.

توجه شود مقدار S در واقع فاصله بین محورهای آرماتورهای عرضی مورب می باشد.

فولاد طولی خم شده

در بسیاری از تیرهای بتن آرمه با بارگذاری متداول، با دور شدن از وسط دهانه و با نزدیک شدن به تکیه گاه ها از مقدار لنگر خمشی مثبت کاسته می شود. در این حالت در نواحی مجاور تکیه گاه ها معمولا ظرفیت میلگردهای طولی موجود در نواحی تحتانی تیر (که برای مقاومت در برابر لنگر خمشی مثبت در مقطع تعبیه شده اند)، بیشتر از مقدار مورد نیاز می باشد.در این شرایط می توان با تعدادی از میلگردهای طولی را در این ناحیه خم نموده و از آنها به عنوان آرماتورهای مقاوم در برابر برش استفاده کرد. همانطور که در شکل زیر مشاهده می شود، این آرماتورها در سه چهارم طول ناحیه میانی خم شده به عنوان آرماتورهای عرضی موثر در نظر گرفته می شوند. در این شرایط زاویه این آرماتورها با محور طولی عضو باید حداقل برابر 30 درجه  باشد.(α≥30)

در این حالت با توجه به اینکه شروع خم میگردهای طولی مورد نظر در چه محلی قرار دارد، حالت های زیر می تواند رخ دهد:

الف)چنانچه آرماتور طولی خم شده شامل یک یا چند میلگرد و یا گروه میلگرد باشد که همگی در فاصله یکسانی نسبت به تکیه گاه خم شده اند، مقدار V_s به صورت زیر محاسبه می شود:

α: زاویه میلگرد طولی خم شده با محور طولی عضو

A_v: مساحت کل میلگردهای طولی خم شده، میلی متر مربع.

f_y: مقاومت تسلیم آرماتورهای طولی، مگاپاسکال.

ب)چنانچه آرماتور طولی خم شده از یک یا چند میلگرد یا گروه میلگرد تشکیل شده باشد که دارای شروع خم های متفاوتی نسبت به تکیه گاه باشند، عملکرد این میلگردهای طولی مشابه میلگردهای عرضی مورب بوده و برای محاسبه مقاومت برشی حاصل از آنها از رابطه گفته شده قبلی استفاده می شود.

باید توجه شود که در این حالت،S برابر فاصله محل خم های میلگردهای طولی در نظر گرفته می شود.

بررسی نکات مهم و کاربردی

1)در بسیاری از سوالات آزمون نظام مهندسی، آرماتورهای عرضی شامل چند نوع آرماتورگذاری با مشخصات قطر، فاصله و یا مصالح مختلف و یا از ترکیب حالات ذکر شده برای V_s می باشد. در چنین مواردی مقاومت برشی اسمی حاصل از آرماتورهای عرضی برابر مجموع مقاومت های برشی هر یک از آرماتورگذاری های عرضی در نظر گرفته می شود. در این حالت می توان مقاومت برشی اسمی آرماتورها را به صورت زیر بدست آورد:

V_si: مقاومت برشی اسمی آرماتورهای برشی در هریک از انواع مصرفی

V_s: مجموع مقاومت برشی اسمی تامین شده توسط آرماتورهای عرضی.

2)مقدار حداکثر مقاومت های تسلیم آرماتورهای عرضی (f_yt) و همچنین آرماتور طولی خم شده مورد استفاده در برش به 420 Mpa محدود می شود، که این موضوع را در جدول فصل اول

بررسی کردیم. در صورتی که شبکه های سیمی جوش شده جایگزین آرماتورهای عرضی گردند، حداکثر مقاومت تسلیم آنها برابر 550 Mpa در نظر گرفته می شود.

در ادامه برای تکمیل مطالب مرتبط با V_s، باید چهار موضوع زیر را نیز در نظر بگیریم و کنترل کنیم:

1)کنترل حداکثر برش قابل تحمل مقطع:

در بخش های قبل با نحوه محاسبه مقاومت برشی اسمی تامین شده توسط بتن و آرماتورهای عرضی آشنا شدیم. همانطور که در بخش اول این قسمت نیز گفته شد، مقاومت برشی اسمی مقطع برابر مجموع مقاومت های حاصل از بتن و آرماتورهای عرضی می باشد. حال سوالی که احتمالا در ذهن شما ایجاد می شود، این است که آیا مقطع می تواند دقیقا به همان مقدار مقاومت برشی اسمی، نیروی برشی را تحمل کند؟ پاسخ قطعا خیر است.

همانطور که از فصل خمش به خاطر دارید، آیین نامه موارده ضریب اطمینانی برای کاهش مقاومت ها به دلیل اطمینان از عدم وقوع گسیختگی های زود هنگام در نظر می گیرد. در این حالت رابطه زیر در حالت نهایی باید برقرار باشد:

V_u: حداکثر نیروی برشی ضریبدار وارد بر مقطع

V_n: مقاومت برشی اسمی مقطع

Φ: ضریب کاهش مقاومت برشی که با توجه به جدول فصل اول برابر 0.75 در نظر گرفته می شود.

علاوه بر کنترل بالا، به دلیل کاهش احتمال گسیختگی های فشاری قطری بتن و همچنین محدود شدن ترک های برشی، ابعاد مقطع باید به نحوی انتخاب شود که در حالت نهایی رابطه زیر برقرار باشد:

بررسی یک نتیجه مفهومی

با توجه به دو رابطه بالا می توان مقدار حداکثری برای V_s به صورت زیر مشخص کرد:

همانطور که مشاهده می شود، رابطه بالا مشابه یک کران بالا برای V_s می باشد. در واقع با این روش آیین نامه تعبیه مقدار بیش از اندازه آرماتور عرضی در مقطع را به دلیل جلوگیری از اعمال تنش فشاری بیش از حد به بتن واقع در فواصل بین خاموت و بروز گسیختگی در این نواحی، محدود نموده است. البته باید به این نکته توجه کرد که در حالت کلی نیازی به کنترل رابطه بالا پس از محاسبه مقاومت برشی آرماتورها وجود ندارد، زیرا رابطه مذکور یک نتیجه ثانویه از رابطه قبلی محسوب می شود. در واقع هدف از کنترل رابطه محدود نمودن برش نهایی وارد بر مقاطع بوده که توسط ابعاد مقطع کنترل می شود. یعنی در مواجه با نیروهای برشی قابل ملاحظه که در رابطه قبلی صدق ننماید، راهکار اولیه برای رفع مشکل افزایش ابعاد مقطع است.

2)مقدار آرماتور حداقل یک مقطع:

مساحت آرماتور عرضی حداقل با صرف نظر از اثرات پیچش، به صورت زیر محاسبه می شود:

در مورد جزئیات آرماتور حداقل، در قسمت سوم فصل به طور کامل بحث خواهیم کرد.

3)محدودیت فواصل آرماتورهای عرضی قائم:

در بخش سوم فصل با نحوه طراحی مقطع در برابر برش و همچنین نحوه محاسبه آرماتورهای برشی آشنا خواهیم شد. در اینجا می خواهیم ضوابط آیین نامه در خصوص فواصل میلگردگذاری عرضی را بررسی کنیم.

هنگامی که میلگردهای عرضی بر اساس نیروی برشی وارده محاسبه می شوند، باید به این نکته توجه کرد که نمی توان آرماتور گذاری را با هر فاصله ای در نظر گرفت. برای عملکرد مناسب مقطع در برابر برش و جلوگیری از وقوع شکست برشی، رعایت حداکثر فاصله بین آرماتورهای عرضی یکی از اساسی ترین نکات طراحی آرماتورهای عرضی می باشد.

حداکثر فاصله مجاز بین آرماتورهای عرضی در راستای طولی عضو و همچنین عرض مقطع بر اساس نیروی برشی تحمل شده توسط فولادها و براساس دو مورد زیر تعیین می شود:

d: عمق موثر مقطع

S_max: حداکثر فاصله بین آرماتورهای عرضی در راستای طولی مقطع

D_max: حداکثر فاصله بین ساق های آرماتور عرضی در عرض مقطع.

برای درک بهتر، پارامترهای S و D در روابط فوق در تصویر زیر نشان داده شده است.

4)محدودیت فواصل آرماتورهای عرضی مایل:

در خصوص خاموت های مایل و یا میلگردهای طولی خم شده، فاصله S باید به نحوی انتخاب شود که هر خط 45 درجه ای که به اندازه d/2 از وسط مقطع در جهت عکس العمل تکیه گاهی به طرف میلگردهای کششی طولی رسم شود، باید مطابق شکل حداقل به وسیله یک ردیف از آرماتورهای برشی قطع گردد.

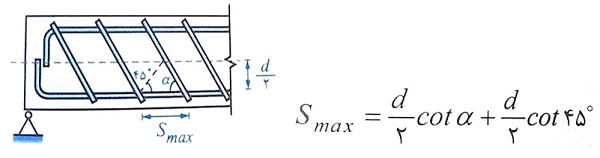
میلگردهای طولی خم شده که به عنوان آرماتور برشی مورد استفاده قرار می گیرند، در صورتی که در ناحیه کششی ادامه داده می شوند، باید همراه آرماتورهای طولی ادامه یابند. چنانچه این آرماتورها در ناحیه فشاری امتداد یافته اند، باید به اندازه طول d/2 از وسط ارتفاع مقطع مهار شوند.

در ادامه با بررسی مثال های متنوع، بر روی نحوه محاسبه V_s به طور کامل مسلط خواهیم شد.

مثال: مقطع نشان داده شده در شکل زیر، مربوط به یک تیر بتنی درجا بوده که در آن بتن از نوع C30 معمولی و فولاد خاموت ها از نوع S400 است. اگر از آثار لنگر خمشی و نیروی محوری بر روی نیروی برشی مقاوم مقطع صرف نظر شود، بدون توجه به الزامات لرزه ای، به موارد زیر پاسخ دهید.

الف)آیا آرماتور حداقل در این مقطع رعایت شده است؟

ب)مقاومت برشی اسمی بتن مقطع برابر چند کیلونیوتن است؟

ج)مقاومت برشی اسمی آرماتورها برابر چند کیلونیوتن است؟

د)حداکثر نیروی برشی قابل اعمال بر مقطع برابر چند کیلونیوتن است؟

حل: آرماتور برشی موجود در مقطع و آرماتور برشی حداقل را به صورت زیر مقایسه می کنیم:

همانطور که مشاهده می کنید، آرماتورهای برشی موجود، آرماتور برشی حداقل را تامین کرده اند.

ب)با توجه به تامین آرماتور حداقل، مقاومت برشی اسمی بتن مقطع برابر است با:

دقت شود که به دلیل عدم حضور نیروی محوری، نیازی به کنترل با V_cmax نمی باشد.

ج)با توجه به اینکه آرماتورهای عرضی به کار رفته در مقطع شامل دو نوع است، با فرض مناسب بودن فاصله بین آرماتورها، V_s را محاسبه می کنیم:

در این مرحله با مقایسه V_s بدست آمده با مقدار 0.33 b_wd فاصله بین خاموت ها و سنجاقی ها را با مقدار مجاز برای آن کنترل می کنیم:

همانطور که مشاهده می کنید، آرماتورهای سنجاقی محدودیت فاصله حداکثر بین آرماتورها را رعایت نکرده اند و به لحاظ منطقی نباید در محاسبه ظرفیت V_s و کنترل آرماتور برشی حداقل لحاظ شوند(البته آرماتور برشی حداقل، بدون سنجاقی ها نیز تامین شده است). با توجه به این موضوع،V_s برابر است با:

V_s=V_s1=364.4 kN

د)حداکثر نیروی برشی قابل اعمال بر مقطع، برابر است با مقدار زیر که با مقدار حداکثر باید کنترل شود.

مثال: در یک تیر بتن آرمه با ابعاد 300×450 mm ، آرماتورهای عرضی از نوع خاموت با مشخصات φ8@200 به صورت مایل و با زاویه 60 درجه نسبت به محور طولی تیر به کار رفته اند. در صورتی که بخواهیم به جای این میلگردها از آرماتورهای قائم بر محور طولی عضو و به قطر 12 mm استفاده کنیم، حداکثر فواصل به کارگیری آنها چند میلی متر می تواند باشد؟ بتن از رده C30 و فولاد S400 و عمق موثر مقطع برابر 400 mm در نظر گرفته می شود.

1- 250                     2- 300                     3- 200                     4- 150 میلی متر

حل: برای انجام این جایگزینی، مقاومت برشی آرماتورهای عرضی در هر دو حالت باید با هم برابر باشند، در این صورت داریم:

بنابراین حداکثر فاصله قابل قبول آرماتورهای عرضی با توجه به 1 و 2 برابر 200 mm بوده و گزینه 3 صحیح است.

مثال: در یک تیر بتنی با مقطع نشان داده شده، برای تامین مقاومت برشی کافی، دو عدد از چهار میلگرد φ25 در فاصله یک متری از تکیه گاه با زاویه 45 درجه خم شده اند. حداکثر نیروی برشی قابل اعمال بر مقطع (بدون در نظر گرفتن اثر آرماتورهای طولی و نیروی محوری) در ناحیه خم بر حسب kN به کدامیک از مقادیر زیر نزدیکتر است؟(فولاد ها از نوع S400 و بتن C25 است. ابعاد روی شکل بر حسب میلی متر است. حداقل میلگرد عرضی برشی در مقطع تعبیه شده است.)

1)416                             2)436                                3)494                             4)500

حل: برای حل این سوال، گام های زیر را طی می کنیم:

گام اول:

با توجه به صرف نظر از اثر نیروی محوری، لذا کنترل شرط V_c≤0.42λ b_wd ضرورتی ندارد.

گام دوم:

مطابق اطلاعات داده شده، آرماتورهای برشی این تیر شامل خاموت های عمود بر محور طولی عضو و همچنین میلگردهای طولی خم شده می باشد. بنابراین مقاومت برشی اسمی مقطع ناشی از آرماتورهای عرضی برابر است با:

دقت شود در تیر مورد نظر، آرماتورهای طولی خم شده همگی در یک فاصله از تکیه گاه خم شده اند، بنابراین مقدار مقاومت برشی آن برابر است با:

گام سوم: مقاومت برشی اسمی و مقاومت برشی نهایی مقطع برابر است با:

همانطور که مشاهده می کنیم مقدار حداکثر V_u بر طرح حاکم شده و گزینه 3 صحیح است. به عنوان تمرین نشان دهید که فاصله خاموت ها کمتر از حداکثر مقدار مجاز است.

بنابراین گزینه 2 صحیح است.

مثال: یک مقطع مستطیلی بتن آرمه را به عرض b_w و عمق موثر d در نظر بگیرید. در صورتی که این مقطع از مصالح معمولی و با بتن رده C40 ساخته شده باشد، به هر یک از سوالات زیر پاسخ دهید. مقطع دارای آرماتور عرضی کافی در نظر گرفته شده و حداکثر نیروی محوری فشاری وارد بر مقطع برابر 20A_g بر حسب نیوتن می باشد.

الف)مقدار حداکثر نیروی برشی قابل اعمال بر این مقطع چقدر می باشد؟

ب)مقدار حداکثر مقاومت برشی که برای آرماتورهای عرضی این مقطع در محاسبات می توان در نظر گرفت چقدر است؟

حل: مقدار حداکثر نیروی برشی از رابطه زیر بدست می آید:

از طرفی مقدار V_c با در نظر گرفتن وجود حداقل آرماتور عرضی در مقطع، به صورت زیر بدست می آید:

مثال: شکل زیر مقطع یک تیر بتن آرمه را نشان می دهد. بتن از رده C25 و معمولی است. همچنین فولاد خاموت ها از نوع S340 است. از اثر آرماتورهای طولی و فشار محوری در تعیین مقاومت برشی صرف نظر شود. حداکثر نیروی برشی که این مقطع می تواند تحمل کند بدون آنکه دچار گسیختگی برشی گردد، چقدر است؟

1)502                     2)376.6

2)574.8                  4)766.4

حل:

با توجه به آنچه گفته شد، به صورت زیر عمل می کنیم:

دقت شود به دلیل صفر بودن نیروی محوری، لزومی به کنترل V_c با V_cmax وجود ندارد.

با توجه به اینکه از دو نوع آرماتور عرضی در مقطع استفاده شده است، بنابراین مقاومت برشی حاصل از آرماتورهای عرضی به صورت زیر محاسبه می شود:

از طرفی مطابق رابطه های گفته شده، مقدار برش نهایی باید در رابطه زیر صدق کند:

با توجه به اینکه 376≤547 است، بنابراین حداکثر نیروی برشی قابل اعمال بر مقطع برابر 376.6 kN خواهد بود.

دقت شود که در این سوال، هر دو آرماتور محدودیت d/4 را رعایت کرده اند و فاصله بین آرماتورهای عرضی قطعا کمتر از مقدار حداکثر است. از طرفی به سادگی می توان نشان داد که آرماتور برشی حداقل نیز در مقطع قرار گرفته است. بنابراین گزینه 2 صحیح است.

مثال: در یک تیر بتنی طره ای برای مقاوم نمودن تیر تحت اثر نیروی برشی از آرماتورگذاری برشی مطابق شکل های زیر استفاده شده است. با فرض یکسان بودن A_sv، S و f_yt در هر دو حالت، نسبت نیروهای برشی مقاوم تامین شده توسط آرماتورها در حالت a به نیروی برشی مقاوم تامین شده توسط آرماتورها در حالت b به کدامیک از مقادیر زیر نزدیکتر است؟ (مقادیر آرماتورهای مصرفی در حد قابل قبول است و راستای نیروی P همواره به سمت پایین است).

1)2                          2)1.4                                    3)1                              4)0.7

حل: در حالت a آرماتورهای عرضی به صورت مایل به کار رفته اند، بنابراین نیروی برشی مقاوم آنها مطابق رابطه زیر که قبلا گفته شده است برابر است با:

در حالت b آرماتورهای عرضی عمود بر محور عضو هستند، بنابراین نیروی برشی مقاوم آنها مطابق رابطه زیر برابر است با:

با توجه به ثابت بودن پارامترهای A_v، f_yt و S در هر دو حالت و با توجه به زاویه 45 درجه آرماتورهای عرضی در حالت a داریم:

بنابراین گزینه 2 صحیح است.

مثال: دو ستون مربعی با مقاطع A و B مطابق شکل های زیر در نظر بگیرید. اگر غیر از آرایش تنگ ها، سایر مشخصات (بارگذاری، ابعاد، رده بتن، سایز، تعداد و نوع میلگردها، فواصل تنگ ها و …) کاملا یکسان باشند، در خصوص مقاومت برشی اسمی این دو ستون، کدامیک از گزینه های زیر صحیح است؟

1)مقاومت برشی هر دو ستون برابر است.

2)مقاومت برشی ستون B بیشتر از A است.

3)مقاومت برشی ستون A بیش از ستون B است.

4)مقاومت برشی هر دو ستون، فقط در بارگذاری های غیر لرزه ای برابر است.

حل: با دقت در شکل های مشخص شده برای ستون ها و با توجه به اطلاعات سوال، مشاهده می شود که تنها عامل تفاوت مقاطع نوع آرماتورهای عرضی آنها می باشد. بنابراین با توجه به یکسان بودن مصالح مصرفی و ابعاد هر دو مقطع می توان نتیجه گیری کرد که پارامتر V_c برای هر دو مقطع ثابت بوده و کافی است مقدار V_s ستون ها با هم مقایسه گردد.

ستون نشان داده شده در مقطع A دارای دو نوع خاموت بسته است که یکی در راستای نیروهای برشی و دیگری به صورت مورب و با زاویه 45 درجه نسبت به نیروهای برشی V_x و V_y قرار گرفته است.

نکته:

در صورتی که خاموت لوزی شکل و یا مثلثی به صورت عمود بر محور طولی مقطع به کار رود، مقدار مقاومت برشی حاصل از آن مطابق رابطه زیر بدست می آید:

α: زاویه آرماتور عرضی مورب با راستای افق.

A_v: مجموع مساحت دو ساق از تنگ لوزی و یا مثلثی شکل.

بنابراین مقاومت برشی حاصل از آرماتورهای عرضی در مقطع A با در نظر گرفتن تنگ بیرونی و همچنین تنگ لوزی شکل داخلی به صورت زیر محاسبه می شود. با توجه به یکسان بودن قطر میلگردهای عرضی، مساحت هر شاخه از آرماتور عرضی برابر A در نظر گرفته می شود.

توجه شود به دلیل مربع بودن مقطع، مقدار α=45 می باشد.

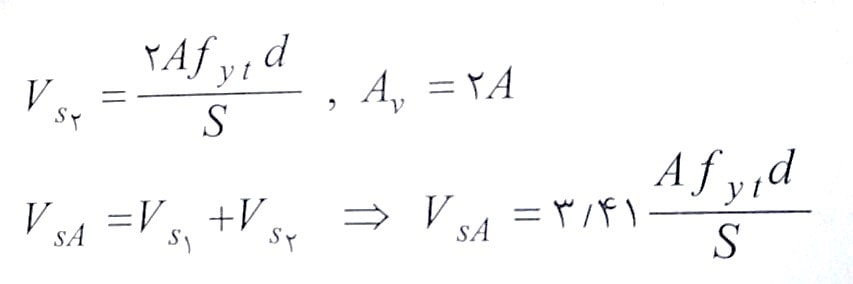
دقت شود مطابق اطلاعات داده شده، مشخصات آرماتورهای عرضی شامل مصالح مصرفی، قطر و فاصله بکارگیری در هر دو مقطع یکسان در نظر گرفته شده است.

در ستون B، خاموت بیرونی دقیقا مشابه ستون مقطع A بکار رفته است. اما سنجاق های متعامد جایگزین خاموت لوزی شکل داخلی شده اند. در واقع تحت نیروهای برشی در راستای x و y فقط سنجاقی که به موازات نیروی برشی قرار گرفته موثر بوده و سنجاق جهت متعامد سهمی در تامین مقاومت برشی ندارد. در این صورت با فرض اینکه مساحت هر ساق از آرماتور عرضی برابر A می باشد، مقاومت برشی حاصل از آرماتورهای عرضی به صورت زیر محاسبه می شود:

با توجه به نتایج بدست آمده، مشخص است که مقاومت برشی حاصل از آرماتورها در مقطع A بیشتر از مقطع B می باشد.

همانطور که در ابتدای حل نیز گفته شد، با توجه به ثابت بودن V_c برای هر دو ستون نتیجه می شود که مقاومت برشی اسمی ستون A بیشتر از ستون B بوده و گزینه 3 صحیح است.

مطلب بعدی: اثر همزمان نیروی برشی در دو جهت

پیج اینستاگرام سیویل 2