سختی سازه یعنی چی

سختی سازه یعنی چی

سختی سازه (STIFFNESS)

سازه هاي مهندسی بايد به نحو ايمني بتوانند در مقابل بارهاي وارده مقاومت نمايند.

در كنار معيار مقاومت, سازه بايد سختي جانبي كافي داشته باشد تا تغيير شكلهاي بيشتر از حد مجاز در آن ايجاد نگردد.

مقاومت و سختي يك سازه بستگي به آرايش هندسي اعضاء ، مشخصات هندسي مقطع  اعضاءومصالح بكار رفته دارد.

مفهوم سختي :

در يك تعريف كلي،مقاومت در مقابل تغيير مكان سختي نام دارد.

 روش محاسبه سختي نيز بدين صورت است كه اگر براي تحليل سازه، تغييرمكانهاي سازگار شامل انتقالها و دورانها به عنوان مجهول انتخاب شوند و سپس شرايط تعادل نيروها در گره هاي سازه اعمال گردد;

معادلاتي بدست خواهند آمد كه مجهولات آنها تغيير مكانها و ضرائب آنها ضرائب سختي ساختمان ميباشد.

تعريف ضريب سختي:

عبارتست از نيروي متناظربا درجه آزادي به ازاي تغيير مكان واحددر درجه آزادي، وقتيكه تغيير مكان در ساير درجات آزادي برابر صفر باشد.

روش شيب افت يك نمونه ازاين روش در تحليل كلاسيك سازه هاست.

همچنين اغلب برنامه هاي موجود تحليل سازه ها بر پايه روش سختي قرار دارد.

انواع سختي ها:

• سختي محوري: سختي محوري ميله اي به طول L وسطح مقطع A ومدول يانگ E
• سختي خمشي : اين سختي تنها تغيير مكانهاي ناشي از خمش را در نظر ميگيرد.
• سختي برشي: اين سختي شامل تغييرمكانهاي ناشي از برش مي باشد. اين سختي براي سازه هاي با تغيير شكل برشي قابل ملاحظه مانند ديوار برشي

سختي سازه

يك سازه به هر دليلي كه مرتعش مي شود تغييرشكل آن يكي از حالات زير يا تركيبي از آنها خواهد بود.

1-تغيير شكل محوري : ارتعاش يك بلوك صلب روي خاك

2-تغيير شكل خمشي: ارتعاش سازه هاي بلند مانند ارتعاش يك دود كش بلند.

3-تغيير شكل برشي: ارتعاش افقي يك ساختمان چند طبقه كه به وسيله تيرهاي صلب كف در ترازهاي مختلف به يكديگر اتصال دارند.

4-تغيير شكل پيچشي: پيچش يك ساختمان با سختي هاي متفاوت

بطور كلي شكل و نوع ارتعاشي يك سازه بستگي به چگونگي پخش جرم و سختي سازه و شرايط تكيه گاهي دارد.

سختي طبقه :

برابر جمع سختي جانبي اعضاء قائم باربر جانبي در يك طبقه است.

براي محاسبه اين سختي ها ميتوان تغيير مكان جانبي واحدي را در سقف طبقه مورد نظر وارد كرد

در حالتيكه كليه طبقات زيرين بدون حركت باقي بمانند.

سختي كل قاب :

برابر جمع سختي جانبي اعضاء  قائم باربر جانبي در تراز مورد نظر است.

براي محاسبه اين سختي ها ميتوان تغيير مكان جانبي واحدي را در سقف طبقه مورد نظر وارد كرد

در حالتيكه دركليه طبقات هيچ قيدي در برابر حركت حركت وجود نداشته باشد.

مركز برش   (center of shear)  :

مركز برش محل برآيند برشهاي يك طبقه است .

مركز پيچش (center of torsion) :

اگر كف تنها تحت اثر يك لنگر پيچشي قرار بگيرد نقطه اي كه تغيير مكان جانبي ندهد مركز پيچش است.

سختی سازه در ایتبس

برای اینکار دو روش کلی وجود دارد:

الف.  از فایل نهایی سازه، فایل های جدیدی به تعداد طبقات تهیه نموده و در هر فایل جهت محاسبه سختی طبقات، پای ستون های طبقه مذکور مقید می شود و در مرکز جرم طبقات یک نیرو به مقدار دلخواه اعمال می گردد.

سپس مقدار جابجایی ایجاد شده در مرکز جرم تحت بار اعمالی را برداشت نمود و با تقسیم نیرو به جابجایی سختی طبقه حاصل می گردد.

ب.  به عنوان روش بعدی که البته در برخی از مراجع بین المللی هم پیشنهاد شده است، می توان از گزینه User Load نرم افزار استفاده نموده که در آن به ازای تعداد طبقات دسته های بارگذاری تهیه می گردد.

در نهایت برای محاسبه سختی، یک نیرو به مقدار دلخواه در تراز طبقه مد نظر وارد کرده و در طبقه زیرین آن دقیقاً مقدار عکس نیروی اعمال شده معرفی می گردد.

با این شرایط دیگر نیازی به معرفی فایل های جدید به تعداد طبقات و مقید کردن پای ستون ها نخواهد بود.

با توجه به اینکه در استانداردهای لرزه ای استفاده از این روش را پیشنهاد کرده اند، بهتر است به جهت ارزیابی سختی طبقات از این روش استفاده شود.

برای محاسبه سختی طبقات در Etabs با روش ارائه شده در بند “ب” بهتر است مراحل ذیل به ترتیب انجام شود:

آنچه از متن های آیین نامه استنباط می گردد؛ به نظر می رسد برای بررسی سختی جانبی طبقات نیازی به کاهش سختی المان های باربر جانبی که از موضوعات مهم روش تحلیل مستقیم در طراحی سازه های فولادی می باشد، نخواهد بود و به همین علت در این بخش از فایل مربوط به کنترل زمان تناوب و نسبت دریفت که با نام project#1-Period-Drift. EDB در مراحل قبلی تهیه شده است، استفاده خواهیم کرد.

معرفی الگوی بار Fx جهت محاسبه سختی طبقات در راستایX

1. در فایل مربوط به زمان تناوب و نسبت دریفت که در آن از کاهش سختی المان های باربر صرف نظرشده است، قفل نرم افزار را باز نموده و از منوی Define گزینه Load Patterns… را انتخاب کنید.
2. در این مرحله قصد محاسبه سختی جانبی طبقات در جهت X سازه را خواهیم داشت. به همین علت در پنچره Define Load Patterns نام الگوی بار را برابر Fx و در ستون Type گزینه Seismic را انتخاب کنید. در ستون Auto Lateral Load گزینه User Loads را انتخاب و در نهایت بر روی گزینه Add New Load کلیک کنیئ تا این الگوی بار همانند شکل ۲-۳۸۸ به نرم افزار معرفی گردد. شایان ذکر است که در صورت نیاز برای کنترل سختی طبقات در راستای Y بهتر است در همین مرحله الگوی بار دیگری مثلاً تحت نام Fy را به نرم افزار معرفی نمایید.

پنجرۀ معرفی الگوی بار Fx جهت محاسبه سختی طبقات در راستایX

نحوه معرفی بار به مرکز جرم برای سختی طبقه Story1,Story2,Story3

3. در ادامه الگوی بار Fx را انتخاب و بر روی گزینه Modify Lateral Load… کلیک کرده تا با پنجره ای همانند شکل ۲-۳۸۹ مواجه شوید.
4. در این پنجره در ابتدا به تعداد طبقات باید دسته بارگذاری معرفی شود. برای این منظور با توجه به اینکه در این پروژه تعداد طبقات برابر ۵ طبقه است، کافیست که در مقابل گزینه Number of Load Sets عدد ۵ ویرایش شود.
5. در هر دسته بارگذاری حتما در مقابل گزینه Additional Eccentricity Ratio (all Diaphragms) عدد صفر را ویرایش کنید. در غیر اینصورت نرم افزار خروج از مرکزیت به مقدار داده شده در این گزینه را نیز در نظر گرفته که مد نظر کنترل این بخش نخواهد بود. همچنین کنترل کنید که گزینه Apply Load at Diaphragm Center of Mass فعال شده باشد تا بار وارد به مرکز جرم طبقات اعمال گردد.
6. در نهایت برای دسته اول در طبقه Story1 مقدار بار ۱۰۰۰ Kgf را در ستون Fx همانند شکل ۲-۳۸۹ معرفی کنید. از این دسته برای محاسبه سختی طبقه Story1 استفاده می شود. در این مرحله فقط به محاسبه سختی در راستای X پرداخته می شود. برای راستای Y نیز دقیقاً باید همین مراحل را طی کرد.

نحوه معرفی بار به مرکز جرم برای سختی طبقه Story1

7. در ادامه همانند شکل ۲-۳۹۰ به دسته دوم بار گذاری (کادر مشخص شده در شکل ۲-۳۹۰) مراجعه کرده و مقدار بار -۱۰۰۰ در ستون Fx برای طبقه Story1 و مقدار بار ۱۰۰۰ برای طبقه Story2 را همانند شکل معرفی کنید. از این دسته بارگذاری برای محاسبه سختی طبقه Story2 استفاده می شود. همچنین در مقابل Apply Load at Diaphragm Center of Mass مقدار صفر را ویرایش کنید. شایان ذکر است اگر که قصد کنترل سختی در راستای Y را داشته باشید، باید مقدار بارها را در ستون Fy معرفی کنید.

نحوه معرفی بار به مرکز جرم برای سختی طبقه Story2 

8. در مرحله بعد به دسته سوم بارگذاری مراجعه کرده و مقداربار بار -۱۰۰۰ در ستون Fx برای طبقه Story2 و مقدار بار ۱۰۰۰ برای طبقه Story3 را معرفی کنید. این دسته بارگذاری سختی طبقه سوم را منتج می نماید که تنظیمات آن در شکل ۲-۳۹۱ نمایش داده شده است. همچنین در این دسته بارگذاری نیز در مقابل Apply Load at Diaphragm Center of Mass مقدار صفر را ویرایش کنید.

نحوه معرفی بار به مرکز جرم برای محاسبه سختی طبقه Story3 

نحوه معرفی بار به مرکز جرم برای محاسبه سختی طبقه Roof 

9. دو دسته بارگذاری ۴ و ۵ را دقیقاً به همین ترتیب به نرم افزار معرفی کنید. در شکل ۲-۳۹۲ دسته بارگذاری پنجم نمایش داده شده است. در نهایت بر روی گزینه OK کلیک کنید. در پنجره Define Load Patterns نیز بر روی گزینه OK کلیک کنید تا دسته بارگذاری جهت محاسبه سختی در راستای X سازه به نرم افزار معرفی گردد.

نحوه معرفی بار به مرکز جرم برای محاسبه سختی طبقه Roof 

سختی طبقات در راستای X

10. در ادامه سازه را آنالیز کنید. پس از پایان مراحل آنالیز سازه، از منوی Display گزینه Show Tables را انتخاب کنید.
11. در پنجره جدید ظاهر شده مسیر Analysis> Results> Structure Results> Story Stiffness را انتخاب کنید.
12. در پنجره جدید ظاهر شده بر روی ستون Load Case کلیک راست کرده و هر ۵ دسته بارگذاری Fx را انتخاب و فیلتر کنید. در نهایت با پنجره ای حاوی اطلاعات مربوط به محاسبات سختی طبقات مواجه خواهیم شد که به جهت راحتی کار، بر روی ستون Shear X کلیک راست کرده و گزینه Sort Ascending را انتخاب نمایید.
13. در ستون Stiffness X سختی طبقات در راستای X گزارش شده است که به جهت راحتی کار، سختی طبقات در جدول ۲-۴۹ ارائه شده است.

سختی طبقات محاسبه شده در راستای X

14. مطابق استاندارد ۲۸۰۰ چنانچه سختی هر طبقه از ۷۰ درصد سختی طبقه بالای خود و یا از ۸۰ درصد متوسط سختی سه طبقه بالای خود کمتر باشد طبقه نرم و چنانچه همین نسبت ها به ترتیب برابر ۶۰ و ۷۰ درصد شود، طبق خیلی نرم در سازه وجود دارد. مطابق جدول ۲-۴۹ سختی طبقات از طبقات پایین به بالا در کاهش است که وقتی چنین وضعیتی در سازه وجود داشته باشد تحت هیچ شرایطی طبقه نرم و یا خیلی نرم در سازه رخ نمی دهد. اما اگر سختی طبقات بالا بیشتر از طبقات پایین باشد باید حتماً به دقت مراحل انجام شده در جدول ۲-۴۹ و در ستون و را انجام دهید. این پروژه مشمول نامظمی سختی جانبی نمی باشد و فرض گرفته شده در ابتدای این فصل کاملاً صحیح خواهد بود.

سختی طبقات در راستای X

تاثیر سختی سازه بر رفتار لرزه ای

افزایش سختی موجب کاهش زمان تناوبمی شود و در نتیجه با توجه به شکل زیر سازه را اگر در ناحیه نرمباشد به سمت ناحیه تشدیدبرده و شتاب پاسخ را افزایش می دهد.

بعکس اگر سازه در ناحیه تشدید باشد، آن را به سمت ناحیه سخت برده و شتاب پاسخ را کاهش می دهد. بنابراین افزایش سختی روی شتاب پاسخ تأثیری دوگانه دارد.

از آنجا که نواحی سه گانه جایگاه ثابتی ندارند نمی توان با قطعیت بیان کرد که آیا سخت کردن یک سازه به افزایش نیروهای زلزلهمی انجامد یا به کاهش آن، به همین دلیل نقش طبقه نرم در یک سازه مدت ها مورد بحث و جدل بوده است.

برخی معتقدند که وجود یک طبقه نرم موجب کاهش سختی و در نتیجه کاهش نیروهای زلزله می شود و گروهی دیگر طبقه نرم را موجب تمرکز انرژی در یک طبقه و در نتیجه انهدام آن طبقه می دانند.

در عمل درستی نظر گروه دوم ثابت شده است و اکنون نظریه اول کنار گذاشته شده است.

گروه اول دو نکته را از نظر دور داشته اند: یکی اینکه با کاهش سختی معلوم نیست نیروهای زلزله کاهش یابد.

اگر چه این مطلب با توجه به طیف آیین نامه درست به نظر می رسد، اما  در طیف آیین نامه ها به دلایلی نیروی زلزله در ناحیه سخت با ناحیه تشدید یکی گرفته شده است. 

دوم اینکه افزایش سختی که معمولاً به کمک بادبند یا دیوار برشی صورت میگیرد با افزایش مقاومت همراه است.

حال حتی اگر بپذیریم که افزایش سختی موجب افزایش نیروی زلزله می شود سؤال این است آیا این افزایش نیرو از آن افزایش مقاومت بیشتر است یا کمتر؟

این سوال در بررسی تأثیر میانقابها بر سختی و مقاومت قابهای مرکب نیز مطرح است.

راه حل این مشکل در این است که ملاک را در جابجایی سازه قرار دهیم نه در نیرو.

اگر با افزایش سختی، جابجایی ها کاهش یابند، سازه در جهت افزایش پایداری حرکت کرده است و برعکس.

بررسی این موضوع به کمک طیف پاسخ جابجایی قابل انجام است که متأسفانه درمقایسه با طیفهای شتاب وسرعت محجور مانده است، چه طیف شتاب برای تخمین نیروهای زلزله و طیف سرعت برای برآورد انرژی زلزله مورد استفاده واقع می شود اما ظاهرا برای طیف جابجایی مصرفی یافت نمی شود.

خوشبختانه برخلاف طیف شتاب، طیف جابجایی از قانونمندی بیشتری برخودار است، به عنوان نمونه طیفهای شکل زیر که برای هشت زلزله مخرب تهیه شده است علاوه بر اینکه به هم شبیه اند، نشان می دهند کاهش سختی همواره موجب افزایش جابجایی است تا انجا که جابجایی به حد خود رسیده  و ثابت می ماند.

از بحثهای فوق می توان نتیجه گرفت که تأثیر افزایش سختی روی نیروهای زلزله گاهی فزاینده و گاه کاهنده است اما روی جابجایی تقریباً همواره اثری کاهنده دارد.

با استفاده از این اصلی میتوان نتیجه گرفت که در یک سازه، عناصر به ظاهر غیرسازه ای نظیر تیغه ها و میانقاب ها به طور نا خواسته سختی و مقاومت را می افزایند و موجب تغییر در نیرو های زلزله و جابه جایی های  مربوطه می شوند.

تاثیر این عناصر بر نیروی زلزله نامشخص است اما جابجایی را تقریبا همیشه کاهش می دهند و از این رو تأثیر مثبتی بر پایداری سازه دارند.

البته آثار ناخوشایندی نظیر سختی نامتقارن که موجب پیچشی و یا افزایشی لنگر واژگونی می شود، مطالبی هستند که باید جداگانه در نظر گرفته شوند. 

چگونگی تشکیل ماتریس سختی کل در نرم افزار المان محدود

همانطور که در مطالب قبل گفته شد روش المان محدود عبارتست از تقسیم قطعه به تعداد زیادی از المانهای کوچکتر و یا به عبارتی شبکه بندی مدل با المانهای مثلثی، مربعی و … که شکل ساده تری نسبت به شکل کلی قطعه دارند.

با ترکیب ماتریس های سختی تک تک المان های یک سازه، ماتریس سختی کل سازه بدست می آید.

به عنوان یک مثال ساده ، سازه ای متشکل از ۲ فنر خطی با سختی K_a و K_b را درحالتی که نیروهای F₁ و F₂و F₃به صورت زیر به آن ها وارد می شود را در نظر بگیرید .

این سازه دارای ۳ درجه آزادی (U₁ و U₂ و U₃) می­باشد. در زیر دیاگرام آزاد هریک از فنرها و ماتریس سختی  آن ها را بر اساس آنچه در مطلب قبل اشاره شده ، مشاهده می نمائید.

با ترکیب ۲ معادله ماتریسی بالا ، معادله زیر حاصل می شود :

با توجه به حالت تعادل استاتیکی در گره ۲ داریم :

بنابراین معادله ماتریسی کل سازه به فرم زیر حاصل می شود :

با توجه به معادله {F} = [K] {U} ، ماتریس سختی کل این سازه برابر است با :

محاسبه ماتریس سختی المان تیر

روش اول: با توجه به اهمیت موضوع و در راستای تکمیل مباحث مربوط به این المان، امروز قصد داریم روش دوم برای استخراج ماتریس سختی تیر (Beam Element) را به شما عزیزان معرفی کنیم.

روش بدست آوردن ماتریس سختی المان تیر

روش دوم: استخراج ماتریس سختی ، بر معادلات انرژی و استفاده از توابع شکل استوار است.

اگر با بحث توابع شکل در اجزای محدود آشنا نیستید توصیه می‎کنم قبل از ادامه بحث، آموزش “المان و تابع شکل در اجزاء محدود” را مرور نمایید.

مطابق شکل زیر، یک المان تیر صفحه‎ ای با خیز، ممان، نیروی برشی و جابجایی گره‎ای مشخص شده را در نظر بگیرید.

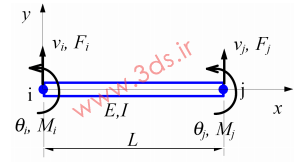
چنانچه مباحث اجزای محدود را دنبال کرده باشید می‎دانید که میزان انرژی ذخیره شده در تیر برابر است با:

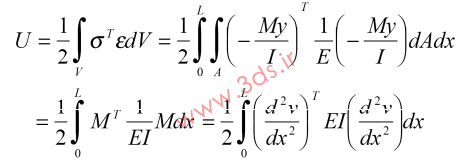
با بازآرایی معادله فوق و استفاده از روابط اجزای محدود داریم:

لذا، ماتریس سختی به کمک این روش، از معادله زیر استخراج خواهد شد:

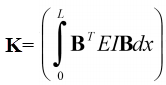
از طرفی، توابع شکل برای المان تیر به صورت زیر معرفی می‎شوند :

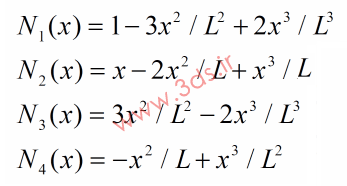
همانطور که مشاهده می‎کنید توابع شکل فوق در گره مربوط به خود دارای مقدار یک (1) بوده و در سایر گره‎ها صفرند و رابطه زیر بین آن‎ها برقرار است:

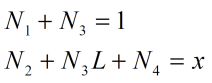
همچنین، تغییر مکان در المان موردنظر بر حسب تغییر مکان گره‎ها از رابطه زیر قابل استخراج خواهد بود:

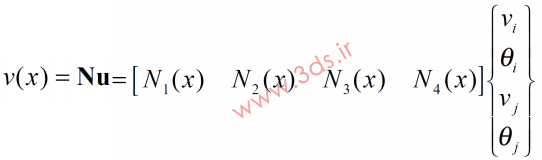
آخرین قطعه از پازل استخراج ماتریس سختی در المان موردنظر به کمک یافتن میزان انحنای تیر تکمیل خواهد شد:

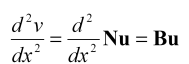
بنابراین، ماتریس کرنش – تغییر مکان (B) در تیر برابر است با:

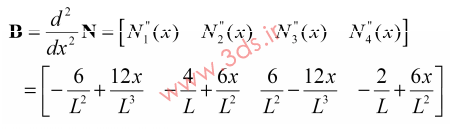
در نتیجه، برای المان تیر داریم:

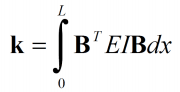
با قرار دادن ماتریس B در معادله فوق و انتگرال‎گیری از آن، ماتریس سختی برای المان تیر (Beam Element) به صورت زیر حاصل خواهد شد:

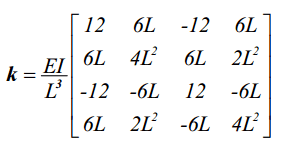
روش بدست آوردن ماتریس سختی قاب (Frame)

تذکر : اتصالات در یک قاب (Frame) به صورت صلب به یکدیگر متصل شده‎اند. در نتیجه، حرکت انتقالی و چرخشی برای اعضای قاب در محل اتصال یکسان خواهد بود.

از این‌رو، در محل اتصال، نیروهای محوری، برشی و ممان خمشی ایجاد می‎شود و لازم است برای تحلیل و مدل‎سازی قاب از ترکیب تیر ساده و المان میله (المان تیر کلی) استفاده گردد.

چنانچه سختی محوری (المان میله) را نیز با معادلات فوق ترکیب کنیم ماتریس سختی برای المان تیر صفحه‎ای در حالت کلی به‎دست می‎آید:

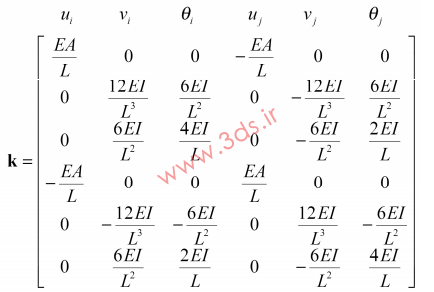
امیدوارم این مطلب مفید واقع شده باشه.

سند بلاست چیست و چه کاربرد و مزایایی دارد؟

پیج اینستاگرام سیویل 2

سختی سازه یعنی چی

سختی سازه یعنی چی

سختی سازه یعنی چی

سختی سازه یعنی چی

سختی سازه یعنی چی

سختی سازه یعنی چی