خرپا استاتیک

خرپا استاتیک

خرپا در استاتیک

خرپا سازه‌ای مثلثی شکل و چند المانی است که تمامی بخش‌های آن به یکدیگر متصل (به صورت مفصلی) شده‌اند.

معنی پین این است که در هیچ مفصلی گشتاوری وجود ندارد؛

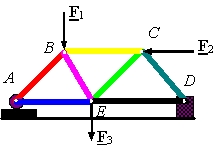
بنابراین در خرپا فقط نیروی محوری وجود دارد. در شکل زیر می‌توانید یک خرپا و نیروهای خارجی وارد شده به آن را ببینید.

خرپا یکی از مباحث موجود در استاتیک رو تشکیل میده و توی صنعت سازه کاربرد فراوان داره.

خرپا سازه‌ای صلب از واحد‌های مثلثی شکل است که از اتصال اجزای باریک و بلند ساخته شده است.

خرپا‌ها توانایی تحمل نیروهای کششی و فشاری را دارند.

دراین گونه سازه‌ها به علت عدم نیروی برشی و لنگر خمشی اتصالات بصورت مفصلی است.

خرپا بر حسب تعریف از مجموعه‌ای از اعضا‌یی بوجود می‌آید که همگی در یک صفحه قرار داشته و ترکیب آنها یک شبکه مثلثی ایجاد نماید.

چون در خرپا‌ها فرض می‌شود که اعضا در انتهای خود به اعضای دیگر لولا شده‌اند بنابر این شکل مثلثی تنها شکل پایدار خواهد بود.

انواع خرپا

1. خرپا ساده simple truss: با اتصال سه عضو در دو گره به صورت مفصلی با یکدیگر یک مثلث تشکیل شده که به آن مثلث بنیادی خرپا گفته می شود.

توسعه خرپا هر بار با اضافه نمودن دو عضو و یک گره صورت می‌گیرد.

اعضای جدید در گره (محل تقاطع دو یا چند عضو را گره می گویند) جدید به یکدیگر مفصل شده و انتهای دیگر آنها به گره‌های موجود مفصل می‌گردند.

خرپاهایی که بدین نحو ایجاد می گردند به خرپاهای ساده موسومند.

2. خرپای مرکب یا Compounded Trusses: خرپای مرکب خرپایی است که از اتصال و ترکیب دو یا چند خرپای ساده ایجاد می گردد.

3. خرپای پیچیده و مبهم: به خرپایی که شرایط خرپای ساده و مرکب را نداشته باشد خرپای مبهم گفته می شود.

مدل های خرپا :

نوع خرپا	شکل خرپا	جنس خرپا	محل استفاده	توضیحات
پرات (Pratt)		معمولا فولاد، در  بعضی موارد چوب	معمولا در سقف و پل	دهانه حداکثر در حدود 30 الی 60 متر
هاو (Howe)		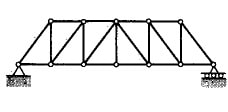معمولا چوب	معمولا در سقف، در گذشته برای سخت پل نیز امورد استفاده بود	دهانه حد اکثر حدود 30 متر
فینک (Fink)		معمولا فولاد	معمولا در سقف	معمولا دهانه در حدود 20 متر
قوسی (Bowst ring)		معمولا فولاد	معمولا در سقف	معمولا برای سقف انبارها و گاراژها، دهانه ممکن است به 30 متر برسد
وارن (Warren)		فولاد	معمولا در پل	دهانه تا حدود 60 متر
پارکر (Parker)		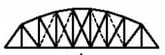فولاد	معمولا در پل	دهانه های حدود 50 تا 100 متر
بالتیمور (Baltimore)		فولاد	معمولا در پل	دهانه های بیش از 100 متر
خرپا ی K) K truss)		فولاد	معمولا در پل	دهانه های بیش از 100 متر

پایداری-ناپایداری-معینی-نامعینی خرپاها

اگر تعداد گره های خرپا را با j و تعداد عضو های آن که همان میله ها هستند رو با m و تعداد عضوهای خرپا رو با R نشون بدیم داریم:
A) اگر m+R<2j باشد خرپا ناپایدار استاتیکیست.
B) اگر m+R=2j خرپا معین است اما پایداری و ناپایداری هندسی آن باید بررسی شود
C) اگر m+R>2j باشد خرپا نامعین استاتیکیست ولی پایداری و ناپایداری هندسی آن باید بررسی شود.

فرمول های تعیین معینی و نامعینی سازه

برای تعیین معین یا  نامعین بودن سازه، از روابط زیر استفاده می گردد:

نامعین ( پایداری باید بررسی شود ) → مجهولات  >معادلات تعادل

معین ( پایداری باید بررسی شود ) → مجهولات= معادلات تعادل

نکته:

ناپایدار → مجهولات < معادلات تعادل

روابط یافتن تعداد معلومات و مجهولات  در دو بعد:

تعداد مجهولات  =  3 برابر تعداد عضو ها در سازه + تعداد مولفه های عکس العمل تکیه گاهی

تعداد معلومات =  3 برابر تعداد مفصل (محل اتصال عضو ها ) + تعداد معادلات شرطی

روابط یافتن تعداد معلومات و مجهولات  در سه بعد:

تعداد مجهولات = 6 برابر تعداد عضوها در قاب + تعداد مولفه های تکیه گاهی

تعداد معلومات = 6 برابر تعداد کل مفصل ها یا گره ها در قاب + تعداد معادلات شرطی

تعیین درجه نامعینی:

اگر تعداد مجهولات را از تعداد معادلات کم کنیم، درجه نامعینی بدست می آید.

خرپای معین و نامعین

توجه داشته باشید که همواره به منظور تحلیل یک خرپا بایستی تعداد معادلات و تعداد نیروها با یکدیگر برابر باشند.

برای بررسی این موضوع اجازه دهید چند نمونه را بررسی کنیم.

شکل زیر را در نظر بگیرید.

می‌خواهیم تعداد نیروهای مجهول در این سازه و تعداد معادلاتی که می‌توان برای آن نوشت را مورد بررسی قرار دهیم.

به نظر شما برای تحلیل این خرپا، چند نیروی مجهول وجود دارد؟

نیروهای مجهول در شکل خرپای بالا:

در حقیقت هر عضو یک نیرو را شامل می‌شود و ۳ عکس العمل تکیه گاه در A و D [یک نیرو در A و دو نیرو در D] وجود دارند.

بنابراین کلا ۱۰ نیرو بایستی محاسبه شود.

هم‌چنین این خرپا از ۵ مفصل تشکیل شده که در هرکدام از آن‌ها می‌توان ۲ معادله تعادل نیرویی، در راستای x و y نوشت.

در نتیجه می‌توان ۱۰ معادله تعادل نیرویی، برای خرپا نوشت.

به طور خلاصه می‌توان گفت: ۱۰ مجهول و ۱۰ معادله برای این خرپا وجود دارد. به چنین سازه‌هایی، معین گفته می‌شود.

حال می‌خواهیم شما را به چالش بکشیم.

بدین منظور خرپای زیر را در نظر بگیرید. به نظر شما در این خرپا چند نیرو وجود دارد؟ همچنین چند معادله می‌توان نوشت؟

نیروهای مجهول در این خرپا عبارتند از:

بنابراین ۹ نیروی مجهول در این خرپا وجود دارد. هم‌چنین معادلاتی را که می‌توان برای این خرپا نوشت به شرح زیر هستند.

این خرپا از ۴ مفصل تشکیل شده که بررای هرکدام از آن‌ها می‌توان دو معادله تعادلی:

و

را نوشت. بنابراین ۸=۲×۴ معادله می‌توان برای این خرپا نوشت.

در نتیجه این خرپا دارای ۹ مجهول است؛ در حالی که می‌توان ۸ معادله برای آن نوشت. به خرپایی که تعداد معادلات آن از تعداد نیروهای مجهولش کمتر باشد، خرپای نامعین گفته می‌شود.

به منظور تحلیل نیرویی خرپای بالا، یکی از عضو‌های AC یا BD بایستی حذف شود [با این کار یک مجهول از معادلات کنار رفته و تعداد مجهولات و معادلات با هم برابر می‌شود].

محاسبه نیرو در خرپا

در حالت کلی به‌ منظور محاسبه نیروهای موجود در یک خرپا از دو روش «مفاصل» (Joints) و «مقاطع» (Sections) استفاده می‌شود.

در هر خرپا با اعمال نیروی خارجی، درون هر عضو نیرویی ایجاد خواهد شد.

برای مثال در خرپای شکل بالا که دو نیروی F_۲ ،F_۱ و F₃ به آن وارد می‌شود، نیروهایی مطابق شکل زیر، در آن ایجاد شده است.

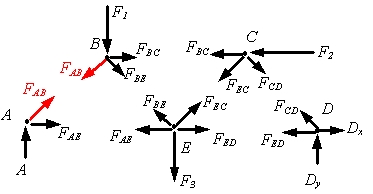
تحلیل خرپا

ابتدا باید با برش دادن خرپا، جزئیات درون مقاطع رو به صورت شماتیک و دیاگرام نیرو مجسم کنیم.

کافیه نسبت به یک نقطه لنگر بگیریم و نیروهای خرپا رو به راحتی محاسبه کنیم.

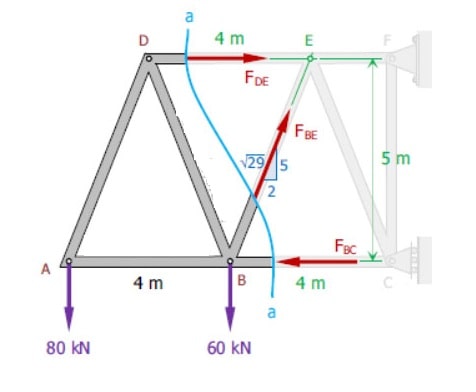
در شکل بالا خرپا از طریق خط آپی رنگ برش خورده است.

نیروهای موجود در خرپا نمایش داده می شود و سپس با لنگر گیری حول نقطه ای مناسب می توانیم نیروهای مجهول خرپا رو محاسبه کنیم.

المان های صفر نیرویی در خرپا

در یک خرپا ممکن است المان هایی وجود داشته باشند که نیرویی را تحمل نکنند.

یعنی هیچ نیروی در عضو خرپا وجود نداشته باشد.

در حقیقت می‌توان خرپا را بدون آن المان تصور کرد. برای مثال در شکل زیر اعضایی که به رنگ آبی، قرمز و صورتی مشخص شده‌اند، نیرویی به آنها وارد نمی شود.

اگر مفصل B و اعضای BC و AB را به صورت دیاگرام آزد ترسیم کنیم به شکل زیر می شود.

اگه دقت کنید برآیند نیروها در راستای محور x و y باید صفر شوند که همینطور هم میشه.

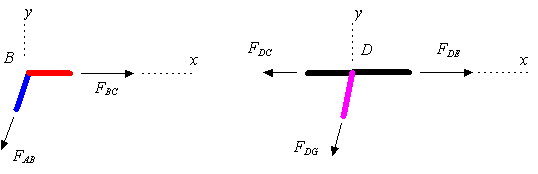
فیلم آموزش خرپا استاتیک:

مثال حل شده خرپا به روش مفصل به زبان ساده

در این بخش مثال حل شده از خرپا ارائه شده است.

یکی از روش های تحلیل خرپا روش گره یا مفصل است. در ادامه یک مثال خوب از این مبحث به زبان ساده ارائه شده است.

فرض کنید قصد داریم برای مثال ارائه شده در شکل زیر نیروهای داخلی هر یک از اعضا را تعیین کرده و اعضای کششی و فشاری را مشخص نمائیم.

نیروی 600 نیوتون به مفصل B خرپا اعمال شده است.

قبل از اینکه بخواهیم نیروهای داخلی اعضا به روش مفصل را محاسبه کنیم، باید عکس العمل های تکیه گاهی را بدست بیاوریم.

تکیه گاه A از نوع مفصلی است و دو عکس العمل دارد و تکیه گاه C غلطکی بوده و فقط یک نیروی عکس العمل دارد.

همانطور که در شکل زیر نشان داده شده است، با نوشتن معادلات تعادل عکس العمل های تکیه گاهی خرپا بدست آمده است.

در ادامه از مفصل A شروع می کنیم و با نوشتن معادلات تعادل استاتیکی برای آن نیرو در عضوهای AB و AC را بدست می آوریم.

ابتدا نیرو در هر دو عضو را کششی در نظر گرفته ایم.

در پایان، چون نیروی عضو AC منفی بدست آمده است متوجه می شویم که نیروی آن فشاری است.

در مرحله بعد با نوشتن معادله تعادل Fx=0 برای مفصل B نیرو در عضو BC هم بدست می آید.

به شکل زیر دقت کنید. چون عدد بدست آمده برای نیروی عضو BC منفی است بنابراین عضو BC هم تحت فشار می باشد.

در شکل زیر نیروهای ایجاد شده در عضوهای خرپا که برای این مثال با روش مفصل بدست آمده است و کششی و فشاری بودن عضوها نمایش داده شده است.

مهار بندی خرپا 

اعضای خرپا لنگر خمشی را تحمل نمی‌کنند و پایداری اعضا در صفحهٔ خرپا توسط گره‌ها تأمین می‌گردد به همین دلیل می‌توان اعضا خرپا را از پروفیل‌های نازک تری ساخت که این موضوع باعث ایجاد مسئله پایداری ارتجاعی می‌شود که برای پایداری خرپا در جهت جانبی از مهاربند استفاده می‌کنند.

اتصالات خرپا 

پس از تعیین حداقل سطح مقطع اعضا، طراحی اتصالات خرپا آخرین گام در طراحی خرپا می‌باشد.

اعضای خر پاها به وسیله جوش، پیچ و مهره ویا پرچ به یکدیگر متصل می‌شوند.

بر اساس نیازهای پروژه، اتصالات خرپا داخلی (مفاصل) می‌تواند به شکل سفت و سخت، نیمه سفت و سخت، یا لولا طراحی شود.

مزایای خرپا فلزی

• مقاوم در برابر نیرو ها‌ی خارجی مانند زلزله
• نصب و اجرای ساده و سریع
• جابه‌جایی و حمل ساده (در مقایسه با سازه‌های بتنی)
• از نظر اقتصادی بسیار مقرون‌ به‌ صرفه
• ایده ‌آل برای ساختمان‌ های مرتفع

کاربرد خرپا در ساختمان ها

برج باو (The bow tower)

برج باو در کشور کانادا و در شهر کلگری قرار دارد.

این برج که دارای ارتفاعی حدود 236 متر است، بلندترین ساختمان در کانادا به شمار می‌رود.

در ساخت این ساختمان مرتفع از سیستم خرپا فلزی دیاگرید استفاده‌شده است.

سیستم دیاگرید عمدتاً در پروژه‌های ساختمانی مرتفع فولادی کاربرد دارد به این صورت که شبکه‌ای از مثلث‌های مورب ایجاد می‌شود.

برای مهاربندی جانبی این ساختمان از خرپاهای مثلثی مورب استفاده‌شده است.

ورزشگاه تیم فوتبال يوونتوس، دل آلپي (Delle Alpi)

این ورزشگاه در سال 2003 در شهر تورین کشور ایتالیا ساخته شد.

در ساخت سقف این ورزشگاه‌ها از سازه خرپا فلزی استفاده‌شده است.

این سازه خرپایی به‌وسیله کابل‌های کششی و دکل دورتادور ورزشگاه مهارشده است.

بهترین روش یادگیری استاتیک در مهندسی عمران 

در پیج اینستاگرام سیویل 2 هر روز آموزش رایگان قرار می گیرد.

خرپا استاتیک – خرپا استاتیک – خرپا استاتیک – خرپا استاتیک – خرپا استاتیک