المان محدود چیست؟

اجزاء محدود چیست؟

روش اجزاء محدود (Finite Element Method – FEM) روشی است که با استفاده از آن می توان بدون نیاز به تحلیل و محاسبات پیچیده و طرفا با مقداری محاسبات ساده ریاضی، مسئله های استاتیک و مقاومت مصالح و… را حل کرده و جواب را به دست آورد. دانستن این نکته لازم است که پایه و اساس این روش، درس محاسبات عددی» است.

اما اصلا این محاسبات عددی» چیست؟ برای جواب به این سوال، باید به چند ترم قبل برگردیم.

ما در ترمهای قبل در درسهایی مثل ریاضی عمومی ۱ و ۲» و همچنین «ریاضی مهندسی» یاد گرفتیم که چگونه مشتق و انتگرال و … را با روش های معمولی حل کنیم.

در درس «محاسبات عددی» یاد گرفتیم که بدون استفاده از روش های معمولی و با استفاده از روش های عددی» می توان «جواب یک انتگرال» یا ریشه یک «معادله درجه سه» را به دست آورد؛

آن هم فقط با تعدادی ضرب و تقسیم و محاسبات ساده ی ریاضی.

اما این نکته را هم فهمیدیم که تنها مشکل «محاسبات عددی» این است که این محاسبات سادهی ریاضی آنقدر طولانی هستند که زمان خیلی زیادی برای حل نیاز دارند.

بنابراین متوجه شدیم که روشهای >>محاسبات عددی» را باید با «رایانه» و نرم افزارهایی مثل متلب و … استفاده کرد؛

زیرا «محاسبات عددی» نیاز به تجزیه و تحلیل پیچیده ندارد و فقط مقدار زیادی» محاسبات سادهی ریاضی است.

تا اینجا مربوط به کاربرد «محاسبات عددی» در رشته ی ریاضی» و دروس مربوط به آن بود. حالا از بحث ریاضی خارج شویم و ببینیم که محاسبات عددی در رشته های مهندسی چه کاربردی دارد؟

رشته ی مهندسی مکانیک به دو شاخه ی «سیالات » و «جامدات » تقسیم می شود.

ما در درس های «ترمودینامیک» و «انتقال حرارت» و «مکانیک سیالات» و… با روشهای معمولی حل مسئله های «سیالاتی» آشنا شدیم.

همچنین در درسهای >>استاتیک» و «مقاومت مصالح» و «دینامیک» هم که مربوط به شاخه «جامدات» بودند، با روش های حل مسائل تنش و کرنش و… آشنا شدیم.

اما نکته ای که وجود دارد این است که به غیر از آن روش های معمولی و سخت که نیاز به تجزیه و تحلیل دارند، روشی دیگر هم وجود دارد که می توان سخت ترین مسئله های ترمودینامیک و «انتقال حرارت» و «مقاومت مصالح» و «دینامیک» را بدون نیاز به تجزیه و تحلیل حل کرد؛

آن هم فقط با مقداری محاسبات سادهی ریاضی. اسم این روش، «شبیه سازی» است.

در رشته ریاضی» به این روش، «محاسبات عددی» می گویند. اما همین محاسبات عددی وقتی وارد رشته ی مکانیک می شود، اسمش تغییر می کند؛

در گرایش «سیالات» به آن «دینامیک سیالات محاسباتی یا CFD» گفته میشود و در گرایش «جامدات» به آن «روش اجزاء محدود یا FEM» می گویند.

در همین درس اجزاء محدود می توان خرپاهای عجیب و غریب را بسیار ساده و فقط با محاسبات ساده ماتریسی تحلیل کرد.

البته اینجا هم مشکلی که هست، «حجم بالای محاسبات ریاضی» است که موجب شده است که از این روش فقط در رایانه ها و نرم افزارهای شبیه سازی استفاده شود.

در گرایش جامدات و درس «اجزاء محدود» از نرم افزارهایی مثل «آباکوس» و «انسیس» و… و در گرایش سیالات از نرم افزارهایی مثل «فلوئنت» و «ای وی ال فایر» و… برای شبیه سازی رایانه ای استفاده میشود.

در این درس مبانی تئوری اجزاء محدود (که نرم افزارهایی مثل آباکوس و انسیس بر اساس آن کار می کنند) بررسی خواهد شد.

انواع المان سازه ها در اجزاء محدود

1- میله ۲- خرپا ۳- تیر ۴- قاب

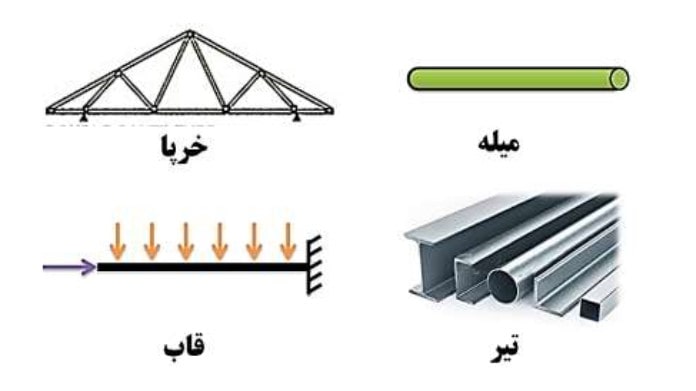
* المان میله ساده ترین المان است و شبیه خرپا است اما با این تفاوت که گرههای میله، جابه جایی عمودی ندارند و ماتریس سختی آن ۲۸۲ است:

گاهی برخی از المان های سازه، فنر هستند که نوعی میله محسوب میشوند.

المان خرپا

خرپا سازه ای است که عضوها المان های آن دو نیرویی هستند و هیچ کدام از المان های خرپا، نیروی برشی یا گشتاور خمشی را تحمل نمی کند.

در دو حالت زیر، به عضو خرپا «صفر نیرویی» گفته میشود:

حالت اول: وقتی به گره 2 نیرو وارد نشود، به عضو2 «صفر نیرویی» گویند.

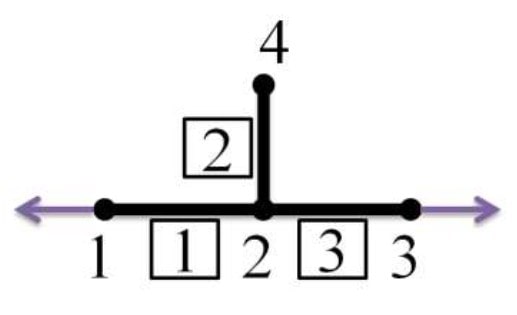
حالت دوم: عضو [1] و [2] «صفر نیرویی» هستند.

هر گره از خرپا دارای دو درجه آزادی است؛ یکی جابه جایی در راستای X (که به آن U می گوییم) و دیگری جابه جایی در راستای Y (که به آن V می گوییم).

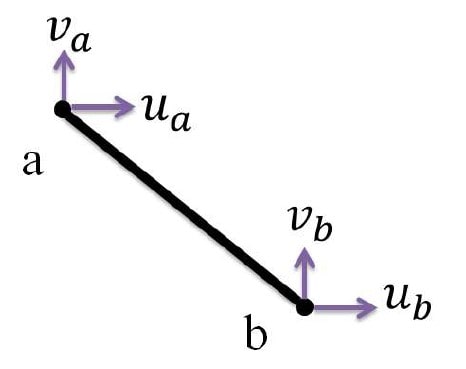
مراحل تحلیل اجزاء محدود خرپا

۱- تشکیل جدول های گسسته سازی (جدول مختصات گرهها و جدول مختصات المانها)

۲- محاسبه ماتریس سختی

3- مونتاژ ماتریس سختی

۴- محاسبه ماتریس نیرو: هر گره، دارای دو درجه آزادی و دو نیرو یکی در جهت X و یکی در جهت Y است. پس ماتریس نیرو برای یک سازه با ۶ گره (m گره) به صورت 12×1(2m x1) است.

۵- اعمال شرایط مرزی: با توجه به صفر بودن جابه جایی بعضی از گره های خرپا، سطر و ستون متناظر با آنها را در ماتریس سختي مونتاژ شده، برابر صفر قرار می دهیم و معادله ی F = [K] A

را حل کرده و جابه جایی های مجهول را به دست می آوریم.

۶- برای محاسبه ی نیروهای داخلی اعضای خرپا کافی است که ماتریس سختي هر المان را در جابه جایی گره های متناظر با آن، ضرب کنیم. با این کار، نیروهای داخلی المان به دست می آیند.

7- معادله مشخصه یک المان خرپا:

المان تیر

المانی است که نیرویی در جهت محوری به آن وارد نمی شود. (اگر نیروی محوری وارد شود، به آن «ستون» گویند و اگر هر دو نیروی محوری و عرضی به آن وارد شود، به آن «تیرستون» می گویند) .

هر گره ی تیر، دارای دو درجه آزادی است؛ یکی جابه جایی در راستای y (که به آن خیز( v) می گوییم و دیگری شیب (Ɵ) است.

در اجزاء محدود، فقط می توان بار نقطه ای با گشتاور وارد کرد و نمی توان بار گسترده اعمال نمود؛

برای رفع این مشکل از ساده سازی زیر استفاده می کنیم:

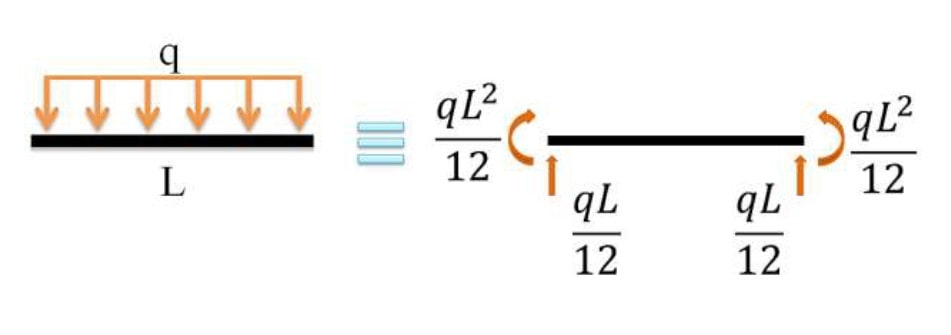
ماتریس سختی تیر:

معادله مشخصه یک المان تیر:

المان قاب

از بین همه ی سازه هایی که تاکنون نام بردیم، قاب از همه کامل تر است و هر گره از المان قاب، دارای ۳ درجه آزادی است: v, u , ,Ɵ

ماتریس سختي قاب، ترکیبی از ماتریس سختی خرپا و تیر است:

معادله مشخصه یک المان قاب:

ماتریس سختی یک المان قاب را باید در ز ضرب کنیم:

اگر توجه شود، برای قابی که افقی است (یعنی 0 = Ɵ است) ماتریس سختی قبل و بعد از ضرب کردن در ماتریس تبدیل، باهم یکسان هستند؛

اما اگر Ɵ≠ 0 باشد، لازم است که برای مونتاژ ماتریس های سختی، آنها را در ماتریس تبدیل ضرب کنیم که نتیجه آن، چنین خواهد بود:

نکته: اگر در یک سازه، یکی از المان ها تیر و یکی قاب بود، برای مونتاژ ماتریس های سختی، باید ماتریس سختی تیر را هم به فرم ماتریس سختي قاب بنویسیم (چون ماتریس قاب از ماتریس تیر کامل تر است)

جمع بندی انواع المان سازه ها

تحلیل تنش صفحه ای برای سازه هایی مانند شکل زیر به کار می رود:

در تحلیل تنش صفحه ای باید نیروها در صفحه قرار داشته باشند و خارج از صفحه (مثلا عمود بر صفحه) نباشند؛ به عبارت دیگر، نیروها اینگونه باید باشند:

و اینگونه نباشند:

رابطه ی زیر بین ماتریس نیرو {F} ، ماتریس سختی [k] و ماتریس تغییر مکان {a} وجود دارد:

{F} = [k]{a}

ماتریس سختی [k] برای المانی به نام e از فرمول زیر به دست می آید:

اکنون به شرح قسمتهای مختلف این فرمول می پردازیم: به ماتریس [D] ، ماتریس خواص می گویند و از فرمول زیر به دست می آید:

که در این فرمول، E مدول یانگ و v ضریب پواسون است و معمولا در صورت سوال داده میشوند. ماتریس [B] از فرمول زیر به دست می آید:

که m ها از فرمول های زیر به دست می آیند:

A مساحت و t ضخامت المان است.

تحلیل کرنش صفحه ای

برای سازه هایی مانند شکل زیر به کار می رود:

در تحلیل کرنش صفحه ای، ماتریس خواص [D] ، از فرمول زیر به دست می آید:

تحلیل تقارن محوری

به شکل زیر توجه کنید:

اگر این مثلث حول این خط، یک دوران ۳۶۰ درجه انجام بدهد، شکل زیر حاصل میشود:

به چنین اجسامی که از دوران یک شکل حول یک «محور تقارن» ایجاد می شوند، اجسام تقارن محوری گفته می شود و برای تحلیل آنها از «تحلیل تقارن محوری» استفاده می کنیم.

به شکلی که حول محور تقارن دوران می کند (که در مثال فوق مثلث است) اصطلاحا «مولد» می گویند.

ماتریس سختی [k] برای تحلیل تقارن محوری از فرمول زیر به دست می آید:

در تحلیل تقارن محوری، ماتریس خواص [D] ، از فرمول زیر به دست می آید:

ماتریس [B] نیز به صورت زیر است:

که مقادیر N از فرمول های زیر به دست می آید:

که مقادیر m نیز به صورت زیر بدست می آیند:

برای دانستن اینکه r_c و z_c در فرمول های بالا چه هستند، به شکل زیر توجه شود:

در شکل بالا، یک مستطیل را به عنوان «مولد» داریم که حول محور تقارن دوران می کند و جسم فوق را ایجاد می کند. اگر مستطیل را المان بندی کنیم، به شکل زیر در می آید:

طبق شکل بالا r_c و z_c مختصات نقطه ی مرکز ثقل المان مثلثی شکل هستند.(توجه شود که مبدا مختصات روی محور تقارن قرار دارد.)

نکته ۱: اگر مختصات سه راس یک مثلث را داشته باشیم، آنگاه می توان مختصات مرکز ثقل را اینگونه به دست آورد:

نکته ۲: اگر اندازه قاعده و ارتفاع یک مثلث را داشته باشیم، آنگاه می توان مختصات مرکز ثقل را اینگونه به دست آورد:

درباره نکته بالا توجه شود که اگر مثلث قائم الزاويه باشد، آنگاه 0 = a خواهد بود و بنابراین:

برای محاسبه ماتریس کرنش یک المان از فرمول زیر استفاده شود:

برای محاسبه ماتریس تنش یک المان از فرمول زیر استفاده شود:

مقایسه بین مرتبه ماتریس های تنش صفحه ای و تقارن محوری

در تنش صفحه ای:

در تقارن محوری :

همچنین ماتریس {a} که ماتریس تغییر مکان است، برای یک المان مثلثی به صورت _6×1{a} است؛ زیرا هر گره دارای دو درجه آزادی است.

بنابراین مرتبه ماتریسهای تنش و کرنش برای تحلیل تنش صفحه ای به صورت زیر:

همچنین مرتبه ماتریس های تنش و کرنش برای تحلیل تقارن محوری به صورت زیر خواهد بود:

جمع بندی:

1- در تحلیل های این فصل نیز مانند فصل های قبل، از رابطه ی { F} = [k]{a } استفاده می کنیم.

۲) ابتدا جداول گسسته سازی (یعنی جدول مختصات گرهها و جدول مختصات المان ها) را تشکیل میدهیم. ۳) سپس از فرمول ^e[k] ماتریس سختی را برای هر کدام از المان ها به دست می آوریم.

۴) سپس ماتریسهای ^e[k] را با هم مونتاژ می کنیم تا ماتریس کلی [k] به دست آید.

۵) اکنون ماتریس تغییر مکان گرهها یعنی {a} و ماتریس نیرو یعنی {F} را با توجه به شکل مسئله می نویسیم و در فرمول { F} = [k]{a } قرار میدهیم.

۶) با توجه به شکل مسئله می بینیم که جابه جایی بعضی از گرهها برابر صفر است؛ بنابراین در رابطه { F} = [k]{a } ، تمام سطر و ستون های متناظر با این جابه جایی ها را حذف می کنیم تا ماتریس ساده تر شود.

۷) حالا معادله ی ماتریسی را به یک دستگاه چند معادله و چند مجهول تبدیل می کنیم و مجهولات مورد نظر را به دست می آوریم.

مثال هایی از المان محدود

مثال: جابه جایی گره ها را در سازه ی زیر بیابید.

جدول مختصات المانها:

جدول مختصات گره ها:

مساحت المان ها:

ماتریس خواص تنش صفحه ای:

برای المان ۱:

برای المان ۲:

با اعمال شرایط مرزی زیر، معادله ساده تر می شود:

معادله ی ساده شده:

المان ها و توابع شکل

المان ها انواع مختلفی دارند:

۱) المان های یک بعدی

۲) المان های دو بعدی

٣) المان های سه بعدی

المان های یک بعدی، خودشان چندین نوع هستند:

المان های یک بعدی دو گره ای (مرتبه ۱)

المان های یک بعدی سه گره ای (مرتبه ۲)

المان های یک بعدی چهار گره ای (مرتبه ۳)

المان های یک بعدی پنج گره ای (مرتبه ۴)

* المان های دوبعدی، به دو نوع تقسیم می شوند:

الف) المانهای دوبعدی مثلثی

ب) المان های دو بعدی مربعی

انواع المانهای دوبعدی مثلثی:

المان مثلثی مرتبه ۱

المان مثلثی مرتبه ۲ سرندیپیتی

المان مثلثی مرتبه ۲ لاگرانژی

المان مثلثی مرتبه ۳ سرندیپیتی

المان مثلثی مرتبه ۳ لاگرانژی

انواع المانهای دوبعدی

مربعی المان مربعی مرتبه ۱

المان مربعی مرتبه ۲ سرندیپیتی

المان مربعی مرتبه ۲ لاگرانژی

المان مربعی مرتبه ۳ سرندیپیتی

المان مربعی مرتبه ۳ لاگرانژی

سوال 1: مرتبه المان یعنی چه؟

جواب: همیشه به ساده ترین نوع المانها، مرتبه ۱ گفته می شود؛ مثلا برای المانهای یک بعدی، المان مرتبه ۱ به صورت زیر است:

و برای المان های دو بعدی مثلثی، المان مرتبه ۱ به صورت زیر است:

و برای المان های دو بعدی مربعی، المان مرتبه ۱ به صورت زیر است:

المان مرتبه ۲ نیز به همین ترتیب است: برای حالت یک بعدی

برای حالت دو بعدی مثلثی:

برای حالت دو بعدی مربعی:

المان مرتبه ۳ نیز به صورت زیر:

برای حالت یک بعدی:

برای حالت دو بعدی مثلثی:

برای حالت دو بعدی مربعی

سوال ۲: المان لاگرانژی یعنی چه؟

جواب: اگر بتوانیم با استفاده از روش لاگرانژ برای یک المان، «تابع شکل» بنویسیم، به آن المان لاگرانژی می گویند.

سوال 3: المان سرندیپیتی یعنی چه؟ جواب: اگر فقط اضلاع المان دارای گره باشند و در داخل المان هچ گره ای وجود نداشته باشد، به آن المان سرندیپیتی می گویند.

اکنون که انواع مختلف المانها مشخص شد، پارامتری به نام «چند جمله ای لاگرانژ» برای هر المان به صورت زیر تعریف می شود: