مشخصات مصالح و مقاطع فولادی

مشخصات مصالح و مقاطع فولادی

برای طراحی اعضای یک سازه فولادی که روابط مختلف آنها را در قسمت های بعدی خواهیم داشت، باید مشخصات مصالح و مقاطع در دسترس باشد.

در این قسمت از آموزش می خواهیم ابتدا مشخصات مصالح فولادی متعارف را برای شما مهندسان عزیز بیان کرده و سپس با انواع پروفیل های فولادی آشنا شویم.

همچنین پارامترهای هندسی مقاطع از قبیل ممان اینرسی، اساس مقطع و … را تعریف کرده و نحوه محاسبه آنها را یاد می گیریم که در قسمت های بعدی به آنها می پردازیم.

مصالح فولادی

آهن ( Fe ) به عنوان یک عنصر شیمیایی، در طبیعت به ندرت به صورت خالص یافت می شود. آهن پر مصرف ترین فلز صنعت است و مصرف آن پیوسته در حال افزایش است.

این عنصر بعد از آلومینیوم فراوان ترین عناصر است و در حدود 5 درصد از قشر جامد کره زمین را تشکیل می دهد.

شکل زیر، نمودار تنش – کرنش چند نوع فولاد متداول را نشان می دهد که در پروژه های ساختمان سازی یا صنعتی کاربرد دارند.

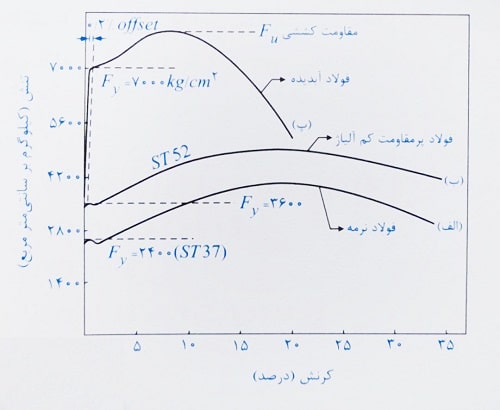
در ناحیه ابتدایی این نمودار که ارتباط بین تنش – کرنش به صورت خطی است، اصطلاحا رفتار مصالح به صورت ارتجاعی ( الاستیک ) است.

تنش نظیر نقطه ای که در آن نمودار به حالت افقی در می آید به تنش جاری شدن یا تسلیم شدن معروف است.

در نمودارهای الف و ب که مربوط به فولادهای نرمه و پرمقاومت کم آلیاژ است، بعد از تنش تسلیم ناحیه ای قوسی شکل وجود دارد که طول آن حدود 15 تا 20 برابر کرنش نظیر حر خطی می باشد.

قله نمودار زیر نیز حداکثر تنش قابل تحمل مصالح را نشان می دهد که تنش نهایی نام دارد.

مشخصات مهندسی فولاد

برای استفاده از روابط طراحی فولاد در مبحث دهم مقررات ملی ساختمان، به برخی از مشخصات مهندسی مصالح فولادی احتیاج داریم که شامل موارد زیر می باشند:

1- ضریب ارتجاعی یا مدول الاستیسیته: همان شیب منحنی تنش – کرنش فولاد قبل از جاری شدن مصالح بوده که با پارامتر E نشان داده می شود. مقدار این پارامتر برای همه فولادهای متداول یکسان بوده و برابر است با:

2- تنش تسلیم و تنش نهایی: تنش تسلیم یا تنش جاری شدن مصالح فولادی با Fy نشان داده شده و تنش نهایی با Fu بیان می شود. مقدار این پارامترها برای فولادهای مختلف متفاوت است، به طوری که برای فولادهای ST37 و ST52 داریم:

نکته: عناوین ST37 و ST52، نام های مرسوم برای فولادهای تولیدی در ایران هستند. در مبحث دهم ملی ساختمان عناوین S235 و S355 برای فولادهای ساخت ایران بیان شده که تنش تسلیم آنها به ترتیب 235MPa و 355MPa می باشد.

لازم به ذکر است که در سوالات، اغلب اطلاعات جدول فوق مورد استفاده قرار می گیرد.

3- ضریب پواسون: این مقدار با پارامتر v نشان داده می شود و برای مصالح فولادی برابر 0.3 است.

4- مدول الاستیسیته برشی: این مقدار با پارامتر G نشان داده شده و از رابطه زیر بدست می آید:

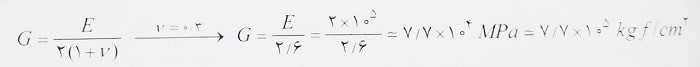
5- ضریب انبساط حرارتی: این مقدار با پارامتر α ( آلفا ) نشان داده می شود و برابر 12×10^-6 می باشد. دقت کنید که برای عضوی به طول L که تحت تغییر دمای ΔT قرار می گیرد، تغییر طول عضو از رابطه ΔL=α(ΔT)L بدست می آید.

آشنایی با پروفیل های فولادی

1- مقطع INP: از گذشته متداول ترین مقطع برای تحمل لنگرهای خمشی در تیرها می باشد. مزیت این مقطع سبکی وزن و ممان اینرسی بزرگ نسبت به محور افقی می باشد.

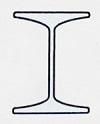
از طرفی این مقاطع دارای ممان اینرسی کم حول محور قائم خود هستند. این مقاطع به صورت تکی برای استفاده به عنوان ستون نامناسب بوده و بایستی به صورت مقطع مرکب به کار روند. به علت شیب بال ها، این مقاطع برای اتصالات پیچی و پرچی مناسب نیستند.

2- مقطع IPE: دارای خواص مشابه INP بوده و کاربرد عمده آن استفاده به عنوان عضو خمشی است. این مقاطع دارای پهنای بال بیشتر بوده و به علت مسطح بودن بال، برای اتصالات پیچی و پرچی مناسب هستند.

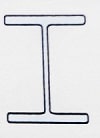
3- مقطع IPB: این نیمرخ ها با نام مقاطع I شکل بال پهن یا H شکل موسوم هستند. عرض بال این مقاطع برای پروفیل های تا عمق 300 میلی متر با عمق مقطع مساوی است.

ممان اینرسی این مقاطع حول دو محور مناسب بوده و نسبت ممان اینرسی حول محور ضعیف به قوی، در این نیمرخ ها بیشتر از این نسبت برای نیمرخ های IPE و INP است. استفاده از این مقاطع به صورت تکی برای ستون ها امکانپذیر است.

4- ناودانی C: این نمیرخ ها تنها دارای یک محور تقارن می باشند و کاربرد آنها به صورت تکی معمولا تولید پیچش می کند. این نمیرخ ها به صورت جفت برای بادبندها کاربرد دارند و به صورت تکی نیز به عنوان لاپه برای پوشش سقف های شیب دار به کار می روند.

همچنین ترکیب ناودانی با مقاطع I شکل برای تولید ممان اینرسی زیاد در سازه های فولادی کاربرد دارد.

5- نبشی L: این نیمرخ به صورت بال مساوی و یا نا مساوی تولید می شود. از این مقاطع برای تقویت ورق های فولادی به عنوان مثال در عرشه های فولادی استفاده می شود. همچنین از این نیمرخ ها برای ساختن شکل های مرکب همراه با نیمرخ های I شکل و ناودانی و نیز در اتصالات استفاده می شود.

6- سپری T: از این نیمرخ بیشتر در ساخت اعضای مرکب و اتصالات سازه های فولادی استفاده می شود.

7- مقطع Z شکل: از این نمیرخ بیشتر در پوشش سقف های شیب دار استفاده می شود. بعضی از کارخانجات فولادسازی اعصایی با نورد سرد با مقاطع به شکل Z و ناودانی تولید می کنند.

8- مقطع لوله و قوطی: از این نیمرخ ها در ساخت ستون ها و مواردی که نیاز به ممان اینرسی بالا حول هر دو محور اصلی است استفاده می شود. این نیمرخ ها به هر دو صورت پی درز و جوش خورده تولید می شود.

9- ریل ها: از این گونه مقاطع برای ریل جراثقال استفاده می شود.

10- ورق های ساده و موج دار: از ورق های ساده برای ساخت مقطع فولادی به صورت تیر ورق استفاده می شود و اتصالات سازه های فولادی و همچنین از ورق های موج دار برای پوشش سقف های مرکب استفاده می شود.

دید مهندسی

به طور کلی اعضای یک سازه با توجه به نوع نیروهای داخلی ایجاد شده در آنها طبقه بندی می شوند. برای استفاده مفید از مصالح، برای هر یک از این اعضاء نیمرخ های مناسبی وجود دارد که درباره مهمترین آنها می توان به موارد زیر اشاره نمود:

• برای ساخت اعضای کششی نظیر خرپا یا اعضای مهار بندی، مهمترین موضوع تامین سطح مقطع کافی می باشد.
• برای اعضای فشاری نظیر ستون ها، باید علاوه بر سطح مقطع مناسب، شعاع ژیراسیون مقطع نیز کافی باشد تا عضو در برابر فشار کمانش نکند. به همین دلیل اغلب از مقاطع قوطی یا دوبل I شکل برای آنها استفاده می شود.
• اعضای خمشی که عمدتا به صورت تیرها شناخته می شوند، باید دارای ممان اینرسی کافی برای تحمل لنگر خمشی باشند. به همین دلیل اغلب از مقاطع I شکل در ساخت آنها استفاده می شود.

پارامترهای هندسی مقاطع در طراحی

به منظور طراحی اعضای یک سازه، همواره از مشخصات هندسی آنها استفاده می شود. این مشخصات شامل پارامترهایی هستند که نحوه توزیع مصالح در مقطع را بیان می کنند و عملا ملاک هایی برای بررسی کارایی و بهره وری مصالح مورد استفاده در مقطع می باشند.

به عبارت دیگر با استفاده از مقادیر این پارامترها، می توان مقاطع را با یکدیگر مقایسه کرد، به طور مثال می توان گفت که مقاومت یک مقطع در برابر لنگر خمشی از مقطع دیگر بیشتر است. مهمترین پارامترهای هندسی مقاطع را که در طراحی سازه های فولادی کاربرد دارند عبارتند از:

1- سطح مقطع ( A )                                                2- محل محور خنثی الاستیک ( Ye )

3- محل محور خنثی پلاستیک ( Yp )                            4- ممان اینرسی ( I )

5- اساس مقطع الاستیک ( S )                                    6- اساس مقطع پلاستیک ( Z )

7- شعاع ژیراسیون ( r )                                             8- اساس مقطع پلاستیک ( Z )

9- ثابت تابیدگی ( Cw )

در ادامه، با نحوه محاسبه هر یک از این پارامترها آشنا می شویم.

سطح مقطع ( A )

سطح مقطع ( Area ) که با پارامتر A نشان داده می شود، دارای بعد طول به توان 2 است ( مثلا mm2 ). این مقدار برابر مجموع سطح مقطع همه قسمت هایی یک مقطع می باشد و به سادگی بدست می آید.

محل محور خنثی الاستیک ( Ye )

محل محور خنثی الاستیک ( Elastic Neutral Axis )، به معنی مکان هندسی نقاطی از مقطع است که دارای تغییر طول نسبی صفر در حین خمش ( کرنش محوری برابر صفر ).

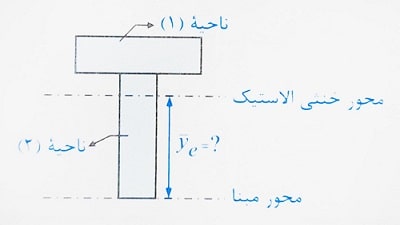
1- یک محور مبنا برای مقطع انتخاب می شود که اغلب تار بالایی یا پایینی مقطع است.

2-محور خنثی الاستیک که مواردی محور مبنا است، در یک محل فرضی در نظر گرفته می شود. فاصله محور خنثی تا محور مبنا را Ye می نامیم که قصد محاسبه آن را داریم.

3- مقطع را به اجزای مستطیلی و ساده تقسیم کرده و آنها را با شماره های 1 تا n نامگذاری می کنیم.

4- حال رابطه زیر را برای اجزای مقطع نوشته و Ye را محاسبه می کنیم.

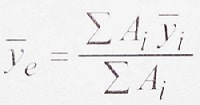
Ai: مساحت جزء i ام مقطع

Yi: فاصله مرکز سطح جزء i ام مقطع از محور مبنا

به طور مثال برای مقطع شکل مقابل که ابعاد آن ذکر شده است داریم:

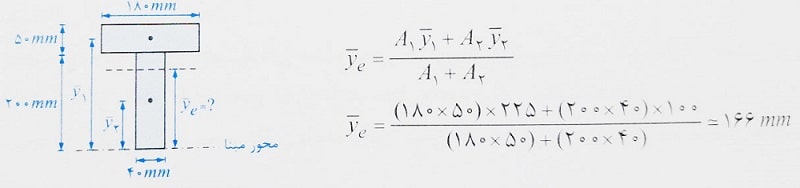
توجه: صورت کسر Ye در حقیقت مجموع لنگر استاتیک اجزای مقطع است، زیرا داریم:

بررسی چند نکته

در تکمیل بحث محور خنثی الاستیک، به چند موضوع زیر توجه کنید:

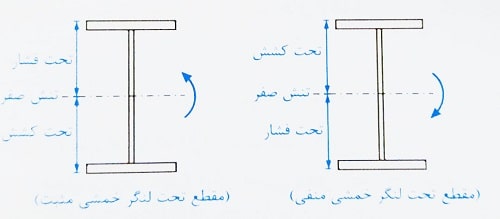
• محور خنثی با توجه به جهت اعمال لنگر خمشی تعریف می شود. از آنجا که معمولا لنگر خمشی وارد بر یک مقطع در دو جهت ممکن است باشد، دو محور خنثی هم برای مقطع وجود دارد که در شکل های زیر مشاهده می کنیم.

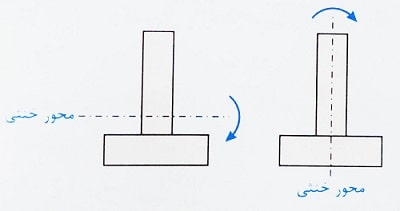
• در صورتی که مقطع دارای محور تقارن باشد، محور خنثی الاستیک همان محور تقارن خواهد بود. این موضوع در شکل سمت راست فوق دیده می شود.
• از آنجا که تغییر طول نسبی ( کرنش ) در محل محور خنثی صفر است، تنش نیز در محور خنثی صفر می باشد. همچنین لازم به ذکر است که جهت تنش ها در دو طرف محور خنثی با یکدیگر متفاوت است که این موضوع را در شکل زیر مشاهده می کنید.

محل محور خنثی پلاستیک ( Yp )

به طور کلی محور خنثی پلاستیک ( Plastic Neatral Axis ) مقطع را به دو بخش با مساحت های برابر تقسیم می کند. به طور مثال در شکل زیر مساحت ناحیه هاشور خورده بالای محور خنثی پلاستیک ( Atop ) با مساحت ناحیه هاشور خورده پایین محور خنثی پلاستیک ( Abot ) برابر می باشد.

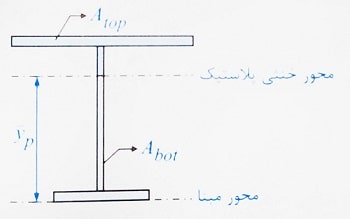
بنابراین قبول دارید که موقعیت محور خنثی پلاستیک و در نتیجه مقدار Yp به سادگی قابل تعیین است.

نکته 1: محور خنثی پلاستیک نیز مشابه محور خنثی الاستیک براساس جهت لنگر خمشی تعریف می شود.

نکته 2: اگر مقطع دارای محور تقارن باشد، محل محور خنثی پلاستیک همان محور تقارن می باشد. در نتیجه اگر مقطع دارای محور تقارن باشد، محور خنثی الاستیک و پلاستیک بر هم منطبق هستند.

مثال: فاصله محور الاستیک و پلاستیک در مقطع زیر چقدر است؟

1- 270.5 میلی متر                         2- 223                                     3- 194.5                                4- 159.5

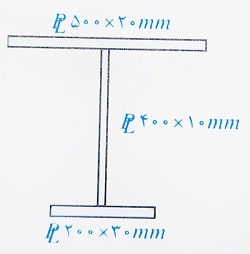
حل: برای تعیین محل محور خنثی الاستیک این مقطع، پایین ترین تار مقطع را به عنوان محور مبنا انتخاب می کنیم و داریم:

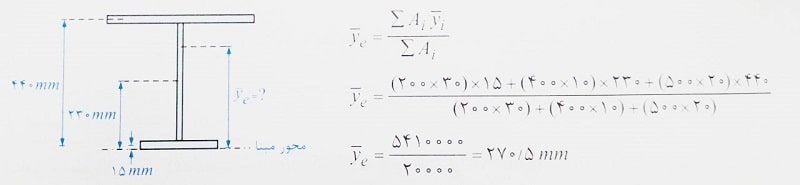
در این تست می توان تنها با نگاه کردن به مقطع و بررسی اولیه آن، محل محور تار خنثی پلاستیک را تعیین نمود.

از یک طرف می دانیم که محور خنثی پلاستیک، مقطع را به دو بخش با مساحت های یکسان تقسیم می کند و از سوی دیگر در این مقطع مشاهده می کنیم که مساحت بال بالایی برابر با مجموع مساحت بال پایینی و کل جان می باشد.

پس محور خنثی پلاستیک در این مقطع، در محل اتصال جان به بال فوقانی قرار دارد. حال می توان به راحتی فاصله بین محور خنثی الاستیک و پلاستیک را در این مقطع محاسبه کرد:

بنابراین گزینه 4 صحیح است.

ممان اینرسی ( I )

ممان ایرنسی ( Moment of Inertia ) یکی از ویژگی های مقاطع است که با پارامتر I نشان داده شده و دارای بعد طول به توان چهار می باشد مثلا ( mm4 ).

به طور کلی ممان اینرسی نسبت به محور خنثی الاستیک محاسبه می شود که درباره آن می توان به حالت ساده زیر اشاره کرد:

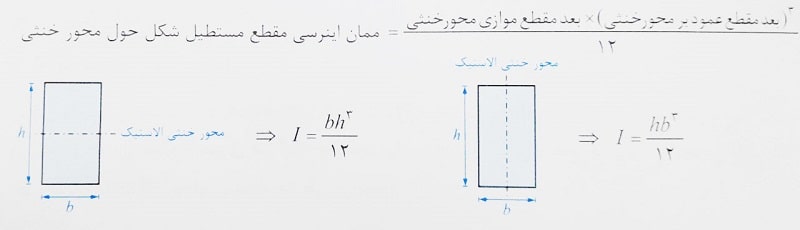
در صورتی که مقدار ممان اینرسی نسبت به محوری غیر از محور خنثی الاستیک نیاز باشد، باید به صورت زیر عمل گردد:

به طور مثال برای محاسبه ممان اینرسی یک مقطع مستطیلی حول ضلع خود داریم:

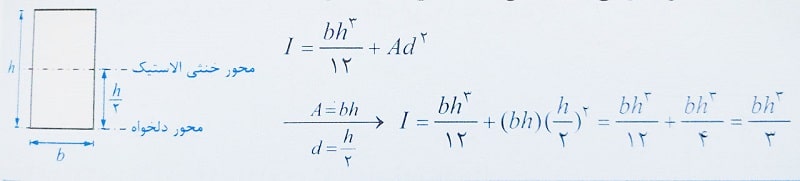
اساس مقطع الاستیک ( S )

اساس مقطع الاستیک ( Elastic Section Modulus یا اختصارا Section Modulus ) با پارامتر S نشان داده می شود و بعد آن طول به توان 3 است ( مثلا mm3).

اساس مقطع الاستیک از تقسیم ممان اینرسی الاستیک ( I ) بر فاصله محور خنثی الاستیک تا تارهای خارجی مقطع ( c ) بدست می آید.

با توجه به اینکه مقدار c در دو سمت محور خنثی حتی ممکن است متفاوت باشد، در حالت کلی دو مقدار برای S بدست می آید. به طور مثال برای مقطع شکل زیر داریم:

نکته 1: اساس مقطع الاستیک، نشان دهنده مقاومت مقطع در برابر لنگر خمشی است که در قسمت های بعدی به آن می پردازیم.

نکته 2: از آنجا که به طور کلی دو مقدار Smin و Smax برای مقطع وجود دارد، دو مقدار برای مقاومت خمشی نیز می تواند محاسبه شود. اما از آنجا که همواره در هنگام طراحی حالت بحراتی تر را در نظر می گیریم، مقدار Smin را ملاک قرار داده تا مقاومت خمشی کمتر محاسبه شود.

اساس مقطع پلاستیک ( Z )

اساس مقطع پلاستیک ( Plastic Section Modulus یا اختصارا Plastic Modulus ) با پارامتر Z نشان داده شده و اساس مقطع خمیری هم گفته می شود. برای محاسبه  اساس مقطع خمیری که بعد آن طول به توان 3 است ( mm3 ) طبق گام های زیر محاسبه می شود:

1- ابتدا باید محل محور خنثی پلاستیک تعیین شود که در بخش های قبل با روش انجام آن آشنا شدیم.

2- مقطع به اجزایی مستطیلی و ساده تقسیم می شود. دقت شود اجزایی از مقطع که محور خنثی پلاستیک از آنها عبور می کند، توسط این تار به دو بخش تقسیم می شوند.

3- مقدار AiYi را برای اجزای مختلف مقطع محاسبه کرده و با هم جمع می کنیم تا اساس مقطع پلاستیک بدست آید بنابراین داریم:

Yi: فاصله مرکز سطح جزء i اُم از محور خنثی پلاستیک

با توجه به گام های گفته شده، برای محاسبه مقدار Z در مقطع شکل زیر داریم:

کمی توجه

همانطور که می دانیم، مقدار AiYi همان لنگر استاتیک جزء i اُم است که با Qi نشان داده می شود. با توجه به این موضوع، می توان رابطه محاسبه Z را برای مقطع شکل بالا به صورت زیر نیز بیان کرد:

مثال: در مقطع شکل زیر، اساس مقطع پلاستیک حول محور قوی تقریبا چند برابر اساس مقطع پلاستیک حول محور ضعیف می باشد؟

1- 3.6                            2-4                          3- 3                                 4- 2.6

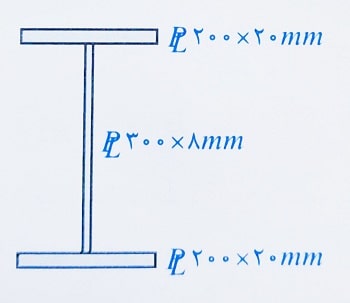
حل: مقطع مورد نظر حول هر دو محور قوی و ضعیف خود دارای تقارن است. پس محل محور خنثی پلاستیک، همان محور تقارن مقطع می باشد. در ادامه می توان مقدار Z را حول هر دو محور مقطع محاسبه کرد. محاسبه Z حول محور قوی:

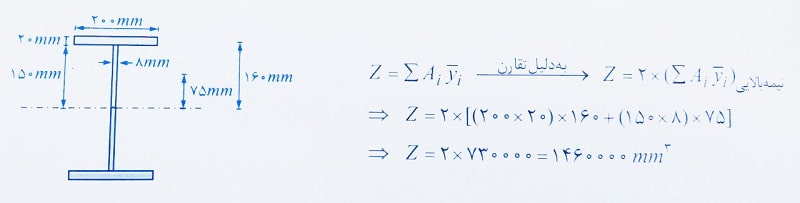
بنابراین گزینه 1 صحیح است.

راهکار دیگر برای محاسبه Z

با توجه به رابطه بیان شده برای پارامتر Z، به سادگی می توان ثابت کرد که رابطه زیر نیز برای محاسبه Z صحیح می باشد:

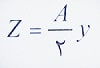
پارامترهای رابطه بالا عبارتند از:

A: کل مساحت مقطع ( در نتیجه A/2 نصف مساحت مقطع که همان مساحت یک طرف محور خنثی پلاستیک است ).

y: فاصله مرکز سطح دو نیمه مقطع که در دو سمت محور خنثی پلاستیک قرار دارند.

برای درک بهتر از نحوه کاربرد رابطه فوق، به مثال زیر توجه کنید. شایان ذکر است که در اغلب موارد استفاده از رابطه Z=Qtop+Qbot ساده تر از رابطه بالایی می باشد.

مثال: اساس مقطع پلاستیک مقطع قوطی مربع شکل فولادی با بعد خارجی یک متر و ضخامت 40 میلی متر حول قطر مقطع بر حسب متر مکعب به کدامیک از مقدار های زیر نزدیک تر است؟

1- 0.018                            2- 0.026                                     3- 0.052                              4- 0.021

حل: اگر سطح مقطع قوطی  A باشد، اساس مقطغ پلاستیک Z برابر است با A/2y که y فاصله از مراکز سطح نیمه های فوقانی و تحتانی مقطع می باشد.

از سوی دیگر مرکز سطح هر یک از جداره های مقطع قوطی شکل زیر در وسط جداره قرار دارد و فاصله آن تا محور  خمش ( قطر افقی ) برابر است با a/2sin45=√2/4a که a بعد متوسط مقطع است و داریم:

نکته: با توجه به محاسبات بالا به راحتی می توان ثابت کرد که اساس مقطع پلاستیک برای یک مقطع قوطی شکل به بعد a و ضخامت t، حول قطر مقطع برابر با 2a2t√ می باشد.

همچنین شایان ذکر است که اساس مقطع پلاستیک این قوطی حول محورهای گذرنده از مرکز سطح آن که موازی وجوه قوطی باشند، برابر با 1.5a2t است.

شعاع ژیراسیون

شعاع ژیراسیون ( Radius of Gyration ) که با پارامتر r نشان داده می شود، دارای بعد طول می باشد ( مثلا mm ).

مقدار شعاع ژیراسیون عبارت است از فاصله محور خنثی مقطع تا یک نقطه فرضی که در آن نقطه می توان تمام سطح مقطع را متمرکز کرد، بدون اینکه تغییری در ممان اینرسی ایجاد شود.

با استفاده از این تعریف اثبات می شود که شعاع ژیراسیون از رابطه زیر تعیین می گردد:

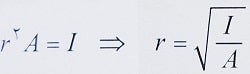
نکته: پارامتر شعاع ژیراسیون، اغلب در محاسبات عضو تحت نیروی محوری فشاری کاربرد دارد و هرچه مقدار آن بیشتر باشد، مقاومت فشاری عضو نیز بیشتر است.

مثال: در یک ورق با مقطع مستطیلی مطابق شکل زیر، شعاع ژیراسیون حول محور قوی به شعاع ژیراسیون حول محور ضعیف برابر است با:

1- t/b                            

2- b/t

3- b2/t2

4- t2/b2

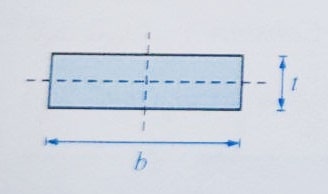
حل: شعاع ژیراسیون، برابر I/A√ است که I و A به ترتیب ممان اینرسی و سطح مقطع می باشند.

بنابرین گزینه 2 صحیح است.

ثابت پیچشی ( J )

ثابت پیچشی ( Torsional Constant ) با پارامتر J نشان داده شده و دارای بعد طول به توان چهار است mm4.

این پارامتر در واقع بیانگر، مقاومت مقطع تحت لنگر پیچشی می باشد. محاسبه دقیق این پارامتر از طریق روابط انتگرالی صورت می گیرد، ولی در مقاطع متداول مانند مقاطع I شکل که دارای اجزای باریک هستند می توان از رابطه زیر استفاده کرد:

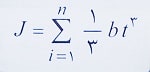
پارامترهای رابطه بالا عبارتند از:

n: تعداد اجزای مستطیل شکل مقطع

b: بعد بلند مدت هر یک از اجزای مقطع

t: ضخامت هر یک از اجزای مقطع

به عنوان مثال، برای محاسبه ثابت پیچشی در مقطع شکل زیر داریم:

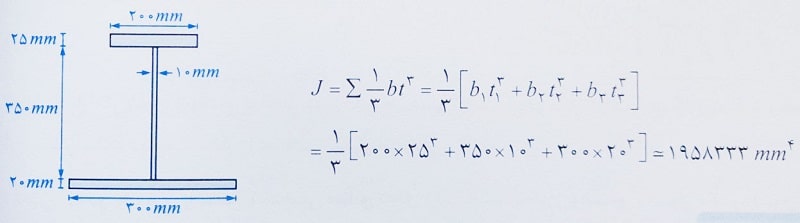
ثابت تابیدگی ( Cw )

ثابت تابیدگی ( Warping Constant ) با پارامتر Cw نشان داده می شود و دارای بعد طول به توان شش mm6 است.

این پارامتر بیان می کند که مقاومت مقطع در برابر پیچش تابیدگی چقدر است.

دقت: پارامتر J در مواقعی کاربرد دارد که لنگر پیچشی باعث ایجاد تنش های برشی در مقطع شود، اما پارامتر Cw هنگامی کاربرد دارد که لنگر پیچشی باعث ایجاد تنش های محوری در مقطع می گردد.

محاسبه مقدار Cw بسیار دشوارتر از J است. برای مقاطع با شکل های خاص روابطی برای مخاسبه Cw پیشنهاد شده است ولی در حالت کلی می توان گفت که برای یک مقطع I شکل و همچنین شکل زیر که از دو ورق هم اندازه با فاصله محور تا محور d تشکیل شده است، ثابت پیچشی به صورت زیر محاسبه می شود:

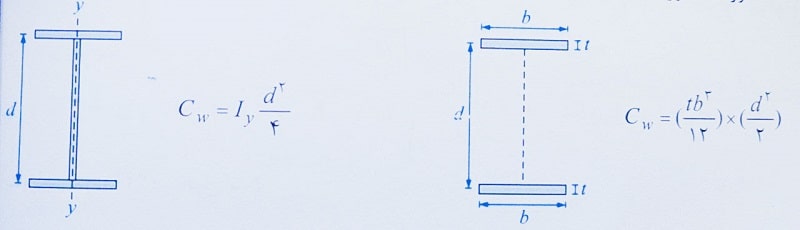
همچنین در شکل های زیر مقدار ثابت تابیدگی برای ند مقطع بیان شده است.

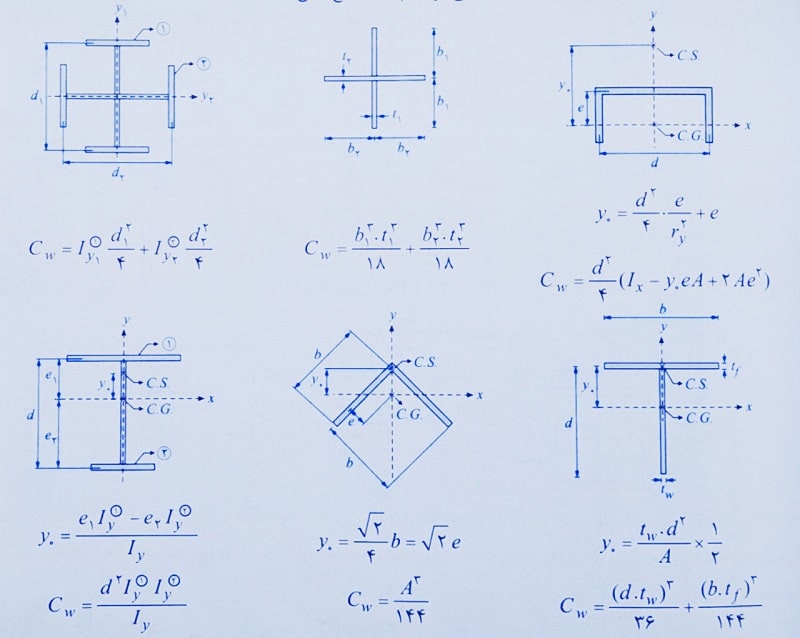
مثال: در شکل زیر، یک مقطع I  شکل از پروفیل IPE360 و یک مقطع صلیبی شکل از دو پروفیل IPE360 نشان داده شده است. مقدار ثابت تابیدگی  مقطع صلیبی شکل چند برابر مقطع I شکل است؟

1- 1                          2- 1.5                    3- 2                                 4- 4

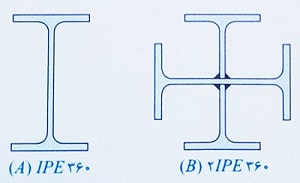
حل: مقدار پارامتر Cw به صورت مجموع Cw برای قسمت های مختلف می باشد. از آنجا که مقطع B از کنار هم قرار گرفتن دو مقطع A ایجاد شده است، مقدار Cw آن نیز دو برابر شده است. بنابراین گزینه 3 صحیح است.

جداول کاربردی مقاطع فولادی

در این بخش قصد داریم چند جدول کاربردی را به شما مهندسان عزیز ارائه کنیم.

جدول پارامترهای هندسی چند مقطع پرکاربرد

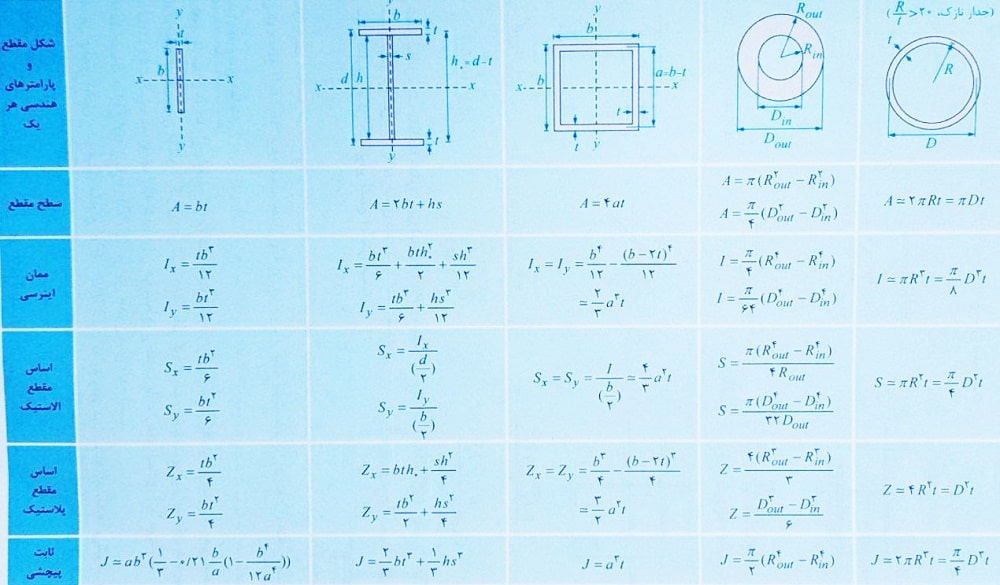
جدول مشخصات مقاطع لانه زنبوری ( مقاطع CPE ) با توجه به شکل زیر

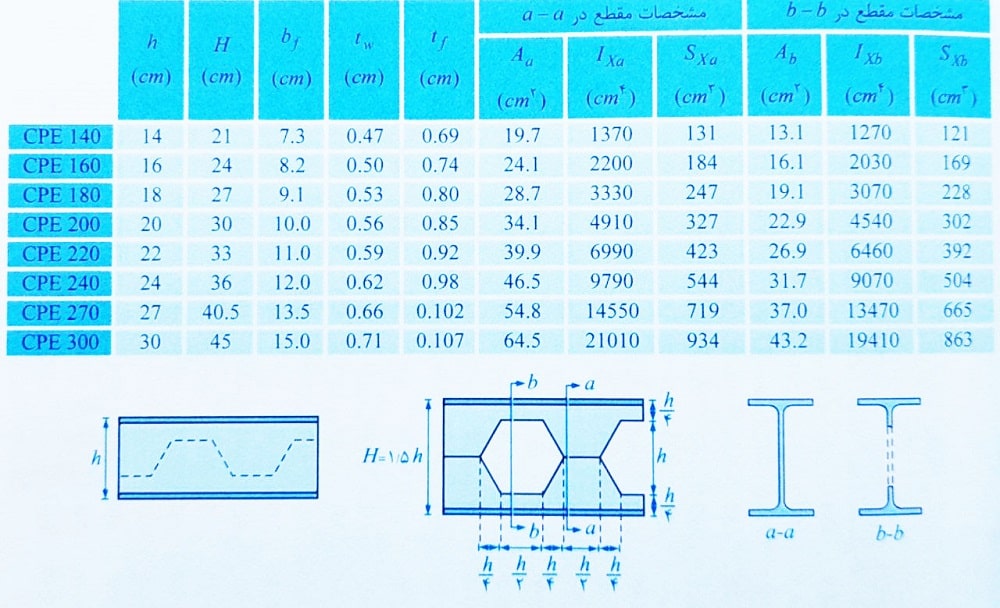
به منظور تسریع روند حل سوالات آزمون نظام مهندسی جدول های زیر پرکاربردتر هستند.

جدول مشخصات مقاطع IPE و IPB

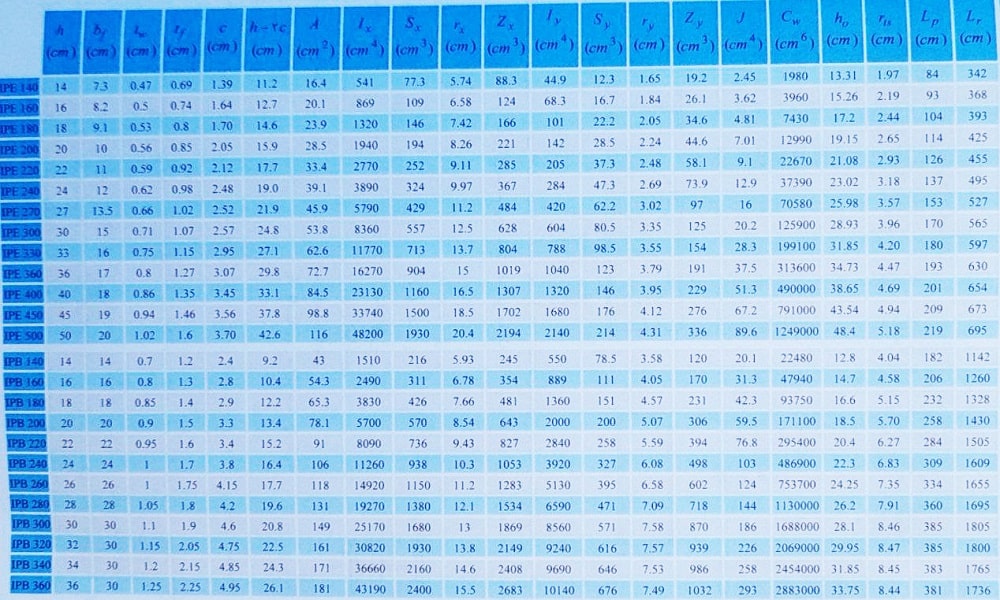
توجه: برخی از پارامترهای ارائه شده در جدول بالا در شکل زیر دیده می شوند:

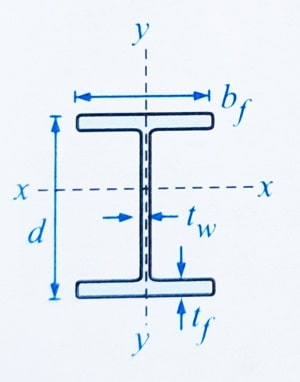
جدول مشخصات مقاطع UNP ( ناودانی اشتال )

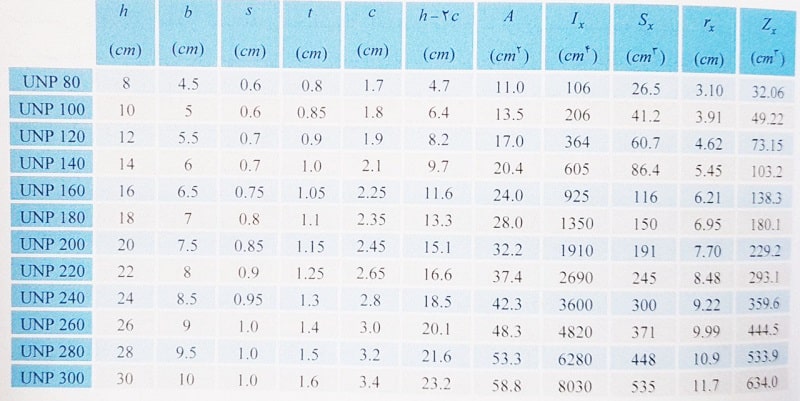
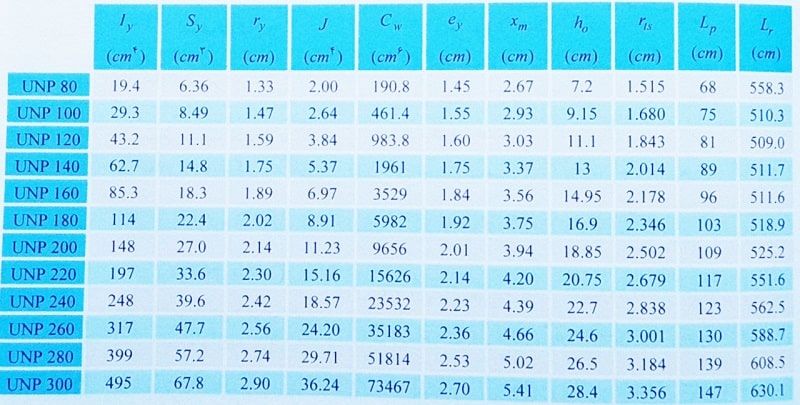
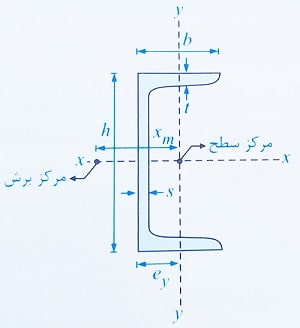
توجه: برخی از پارامترهای ارائه شده در جدول بالا در شکل زیر دیده می شوند:

اصول تبدیل واحدها

مهندسان برای بیان مقدار کمیت های مختلف، از واحدهای مرتبط با آن پارامتر استفاده می کنند. به طور کلی سیستم واحد اصلی در میان مهندسان عمران متداول است که در جدول زیر ارائه شده است و واحدهای آنها نیز برای چند پارامتر بیان شده اند.

دقت داشته باشید که مبحث دهم مقررات ملی ساختمان ویرایش 13692 و تست های مطرح شده واحد SI مورد استفاده قرار می گیرد.

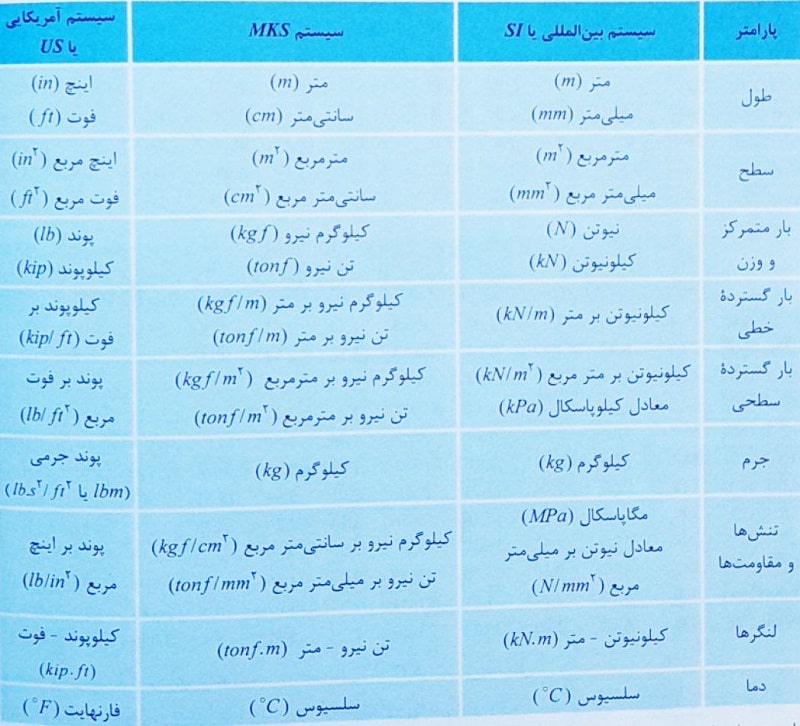
برای تبدیل واحدها مختلف به یکدیگر باید تناسب بین آنها برای شما مهندسان عزیز مشخص باشد. در اینجا مهمترین موارد لازم  برای تبدیل واحدها را بیان می کنیم:

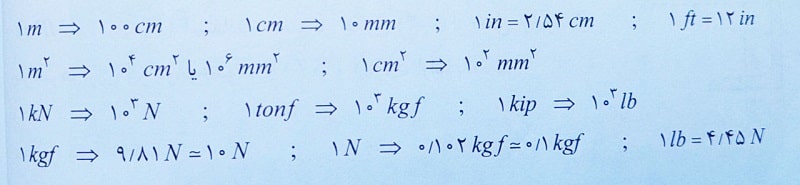
حال برای درک بهتر شما مهندسان عزیز، قصد داریم دو تبدیل واحد زیر را انجام دهیم. برای انجام هر یک از این موارد، کافی است پارامترهای مورد نظر را یک به یک و با توجه به تناسبات گفته شده، تبدیل کنید.

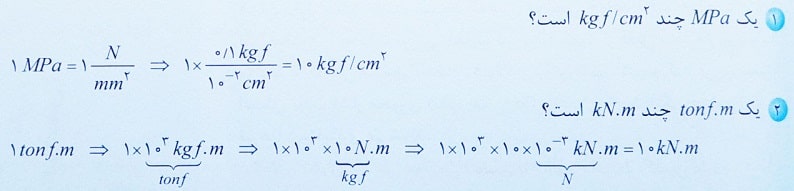
توجه: معمولا در عرف مهندسی، به جای kgf و tonf از kg و ton استفاده می شود. هر چند این موضوع از نظر علمی دارای اشکال است، ولی با توجه به متداول بودن، آن را می پذیریم.

پیج اینستاگرام سیویل 2

مشخصات مصالح و مقاطع فولادی – مشخصات مصالح و مقاطع فولادی – مشخصات مصالح و مقاطع فولادی – مشخصات مصالح و مقاطع فولادی – مشخصات مصالح و مقاطع فولادی