بررسی وضعیت مقطع در حالت شکست نرم

تعریف حالت پلاستیک

وضعیت پلاستیک در مقاطع اعضای خمشی بیانگر حالتی است که در آن مقاومت بتن و فولاد به حد نهایی خود رسیده و با توجه به جزئیات هندسی، آرماتور گذاری و مشخصات مصالح به کار رفته در مقطع، بیشترین مقاومت خمشی مقطع در این ناحیه بدست می آید.

لنگر خمشی حداکثر قابل تحمل مقطع در این حالت مقاومت خمشی مقطع نامیده شده و مقدار آن با توجه به پارامتری به نام لنگر خمشی اسمی مقطع که با M_n نمایش داده می شود، به دست می آید.

در این بخش ابتدا روابط محاسبه لنگر خمشی اسمی مقطع در حالت شکست نرم را با حل مثال های متنوع شرح می دهیم.

گام های محاسبات

1- با توجه به توزیع تنش ویتنی، نیروهای کششی و فشاری مقطع در حالت شکست نرم را چگونه بدست می آوریم؟

در حالت شکست نرم، فولادها قطعا جاری شده اند. در ادامه با توجه به شکل رسم شده زیر برای محاسبه نیروهای کششی و فشاری کافیست حاصلضرب تنش وارده در مساحت تحت تاثیر آن محاسبه گردد:

تذکر:

از بتن واقع در ناحیه کششی مقطع به دلیل ترک خوردگی صرف نظر می شود. بنابراین برای محاسبه نیروی کششی فقط اثر آرماتورهای واقع در این ناحیه در نظر گرفته می شود.

2- ارتفاع بلوک فشاری تنش مستطیلی چقدر است؟

به کمک رابطه T=C به سادگی ارتفاع بلوک ویتنی a رابدست می آوریم:

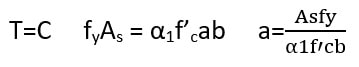
3- لنگر خمشی اسمی مقطع چگونه محاسبه می شود؟

همانطور که می دانیم نیروهای کششی و فشاری مقطع دو نیروی مساوی و مختلف الجهت هستند که باعث ایجاد یک کوپل می شوند. در این صورت لنگر خمشی ناشی از حاصلضرب نیرو در بازوی لنگر همان لنگر خمشی اسمی مقطع می باشد:

با توجه به مقدار ارتفاع بلوک فشاری به سادگی می توان مقدار X را به صورت زیر بدست آورد:

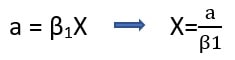
کرنش در فولاد (Ԑ_s) نیز به سادگی با تشابه در نمودار کرنش محاسبه می شود:

مثال: شکل زیر مقطع یک عضو خمشی را نشان می دهد. با توجه به ابعاد مشخص شده بر روی شکل چنانچه بتن از رده C30 و فولاد S400 و آرماتورهای طولی مقطع شامل 4φ20 باشد به سوالات زیر پاسخ دهید:

الف) عمق محور خنثی در لحظه نهایی در این تیر چقدر است؟

ب) ظرفیت خمشی اسمی مقطع چند کیلو نیوتن متر است؟

ج) در صورتی که رده بتن از C30 به C70 تغییر یابد عمق محور خنثی و ظرفیت خمشی اسمی مقطع چگونه تغییر می کند؟

حل:

الف) با توجه به صورت سوال ابتدا باید به صورت زیر ارتفاع بلوک ویتنی را بدست آوریم:

ج) با تغییر رده بتن از 30 به 70 پارامترهای α₁ و β₁ تغییر می کنند ( از جدول قابل برداشت هستند):

مثال: در یک تیر بتن آرمه با مقطع مستطیلی تک آرمه، روند افزایش یا کاهش ظرفیت خمشی اسمی مقطع در لحظه نهایی را با تغییر هر یک از پارامترهای زیر بررسی کنید:

الف) افزایش f’_c

ب)افزایش مساحت آرماتورهای کششی مقطع

ج) افزایش عرض مقطع

د) افزایش عمق موثر مقطع

حل:

قبل از حل سوال باید بدانیم که در تحلیل سوالات خمش تک آرمه در حالت شکست نرم، تغییرات پارامتری که تنها بر روی عمق بلوک فشاری (a) تاثیر گذار باشد و مقدار نیرو را تغییر ندهد، تاثیر ناچیزی بر روی لنگر خمشی اسمی مقطع دارد.

مثال: در یک مقطع مستطیلی (b=30 cm و d = 50cm) تحت اثر لنگر خمشی چنانچه آرماتورهای کششی 4φ20 و رده بتن از C25 و رده فولاد S400 باشد، فاصله محور خنثی در حالت حدی نهایی از دورترین تار فشاری مقطع به کدام یک از اعداد زیر بر حسب mm نزدیک تر است؟

1)93 2)133 3)105 4)79

با توجه به اینکه مقطع در حالت نهایی قرار گرفته است، بنابراین باید مقدار عمق محور خنثی را با استفاده از پارامتر عمق بلوک فشاری و با استفاده از رابطه تعادل محاسبه نماییم:

مثال: در مقطع یک عضو خمشی مطابق شکل ( d=50 mm و b=300 mm) در صورتی که بتن از رده C30 و فولاد از نوع S400 با سطح مقطع A_s = 4φ20 باشد، تغییر شکل نسبی فولاد در حالت حدی نهایی (هنگامی که تغییر شکل نسبی بتن در دورترین تار فشاری به 0.003 می رسد). به کدام یک از اعداد زیر نزدیک تر است؟ (توزیع تغییر شکل نسبی در ارتفاع مقطع به صورت خطی می باشد.)

1)0.016 2)0.002 3)0.005 4)0.014

حل:

برای محاسبه Ԑ_s به صورت زیر عمل می کنیم:

گزینه 1 صحیح است.

مثال: با فرض خطی بودن توزیع کرنش در ارتفاع مقطع تیر با شکل زیر، کرنش فولاد تحت لنگر خمشی اسمی مقطع به کدامیک از مقادیر زیر نزدیک تر است؟ بتن از رده C70 و رده فولاد میلگردها S400 و E=200 GPa می باشد. در محاسبات از آرماتور فشاری صرف نظر گردد. ابعاد به میلی متر و پنج میلگرد پایین تحت کشش هستند.

1)0.0152 2)0.0028 3)0.0020 4)0.0162

حل:

با توجه به اینکه طراحی مقاطع خمشی بر اساس وقوع شکست نرم صورت می گیرد، ابتدا عمق بلوک فشاری ویتنی را به صورت زیر بدست می آوریم:

گزینه 4 صحیح است.

در ادامه به بررسی مسائلی می پردازیم که در آنها انحنا برای مقطع شکست در حالت نرم مورد بررسی قرار می گیرد. یاد آوری می شود که انحنا مقطع شیب نمودار کرنش نسبت به محور قائم می باشد.

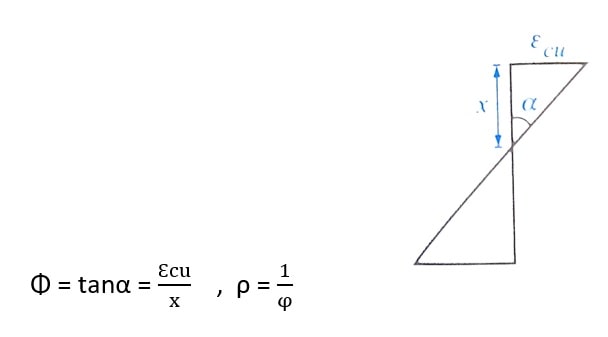
مثال: در مقطعی از یک تیر بتن مسلح بر اثر لنگر وارده، به طور همزمان کرنش در دورترین تار فشاری به 0.0025 و در مرکز میلگردهای کششی به 0.0030 رسیده است. اگر عمق موثر تیر برابر 500 mm باشد، شعاع انحنای تیر در آن مقطع حدودا چند متر خواهد بود؟

1)200 2)167 3)91 4)1000

حل: با توجه به اطلاعات داده شده می توان نمودار کرنش ها را به صورت زیر رسم کرد. در این صورت با محاسبه عمق محور خنثی به راحتی می توان مقدار انحنا و شعاع انحنا را بدست آورد. دقت شود که شیب نمودار کرنش نسبت به محور قائم برابر انحنای مقطع است:

مثال: یک تیر بتنی مستطیلی تک آرمه با عرض 400 و ارتفاع موثر 450 میلی متر مفروض است. فولاد S400 و بتن C25 بوده و مساحت آرماتورهای به کار رفته نیز 3000 mm² می باشد. اگر بخواهیم در این تیراز بتن رده C70 استفاده کنیم، شعاع انحنای مقطع در حالت نهایی چند متر کاهش می یابد؟

1)16 2)23 3)26 4)28

حل:

مطابق آنچه خواندیم می دانیم با افزایش مقاومت فشاری بتن، مقدار عمق محور خنثی با ثابت بودن سایر پارامترها کاهش می یابد. برای محاسبه این مقدار با استفاده از رابطه تعادل خواهیم داشت:

مثال: برای افزایش شکل پذیری تیر بتن آرمه در لحظه نهایی، انتخاب کدام یک از گزینه های زیر مناسب تر است؟

1- افزایش f’_c_،کاهش f_y، افزایش A’_s، کاهش A_s

2- افزایش f’_c_،افزایش f_y، کاهش A’_s، افزایش A_s

3- کاهش f’_c_،افزایش f_y، کاهش A’_s، افزایش A_s

4- کاهش f’_c_،کاهش f_y، افزایش A’_s، کاهش A_s

حل:

برای افزایش شکل پذیری کافیست مقدار انحنای تیر که معادل با شیب نمودار کرنش است افزایش یابد. با توجه به رابطه محاسبه انحنا داریم:

همانطور که مشخصه f’_c با a رابطه عکس دارد و با افزایش f’_c مقدار a و در نتیجه x کاهش می یابد.

مقدار a با f_y رابطه مستقیم دارد بنابراین با کاهش f_y مقدار a و سپس x کاهش می یابد.

با افزایش A’_s به مقطع، بخشی از نیروی فشاری بر بتن به آرماتور فشاری منتقل شده، به همین دلیل با توجه به ثابت بودن نیروی کششی، محور خنثی به سمت بالا حرکت کرده تا با کاهش نیروی فشاری بتن، تعادل مجددا در مقطع برقرار شود. بنابراین در این حالت نیز مقدار x کاهش می یابد.

با کاهش مساحت فولادهای کششی A_s مقدار a و سپس x نیز کاهش می یابد.

گزینه 1 صحیح است.

بررسی مثال های متنوع از خمش در مقاطع گوناگون

مثال: در صورتی که مقدار آرماتور خمشی در هر دو مقطع شکل زیر برابر A_s = 4φ20 باشد، نسبت لنگر خمشی اسمی مقطع A به لنگر خمشی اسمی مقطع B به کدامیک از اعداد زیر نزدیک تر است؟ ( بتن از رده C30 و فولاد S400 می باشد).

1)1.20 2) 0.8 3)1.1 4)0.9

حل:

روش اول: با توجه به یکسان بودن مشخصات مصالح و مقدار آرماتور کششی در هر دو مقطع، تنها عامل اختلاف در ظرفیت خمشی دو مقطع، مقدار بازوی لنگر می باشد. با توجه به این نکته برای بدست آوردن پاسخ صحیح ابتدا با استفاده از رابطه تعادل، عمق بلوک فشاری را در هر حالت محاسبه نموده، سپس مقدار بازوی لنگر را بدست می آوریم:

با تعیین مساحت بلوک فشاری کافیست در هر یک از مقاطع با توجه به هندسه، ارتفاع ناحیه فشاری را بدست آوریم:

حالت A:

در این مرحله برای بدست آوردن مقدار بازوی لنگر باید محل مرکز سطح ذوزنقه هاشور خورده را بدست آوریم. اما به دلیل اینکه سوال به صورت تقریبی مطرح شده است، می توانیم این سطح را مانند مستطیل در نظر گرفته و مرکز سطح را همان a/2 فرض کنیم (به عنوان تمرین محل دقیق را محاسبه کنید و با پاسخ داده شده مقایسه کنید).

حالت B:

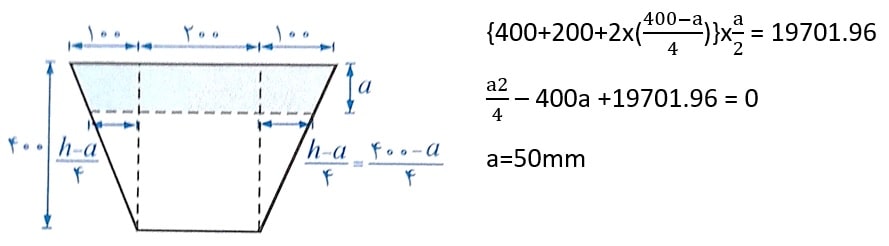
همانطور که گفته شد نسبت ظرفیت خمشی دو مقطع با نسبت بازوی لنگر آنها رابطه مستقیم دارد، بنابراین با فرض قرار گرفتن مرکز سطح دو ذوزنقه در وسط آنها داریم:

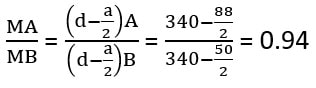
روش دوم: با توجه به یکسان بودن مشخصات مصالح و مقدار آرماتور کششی در هر دو مقطع، تنها عامل اختلاف در ظرفیت خمشی دو مقطع، مقدار بازوی لنگر به دلیل اختلاف در عرض ناحیه فشاری دو مقطع می باشد. به همین دلیل برای محاسبه نسبت لنگرهای خمشی، کافیست عمق بلوک های فشاری را محاسبه کنیم. از طرفی به دلیل اینکه سوال به صورت تقریبی مطرح شده است، به منظور سهولت در حل مقاطع می توان مقاطع را به صورت مستطیلی با عرض های ثابت 200 و 400 میلی متر در نظر گرفت (همانطور که گفتیم تاثیر تغییر عرض در لنگر خمشی مقطع ناچیز است):

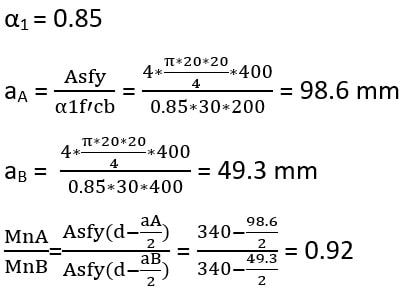
گزینه 4 صحیح است.

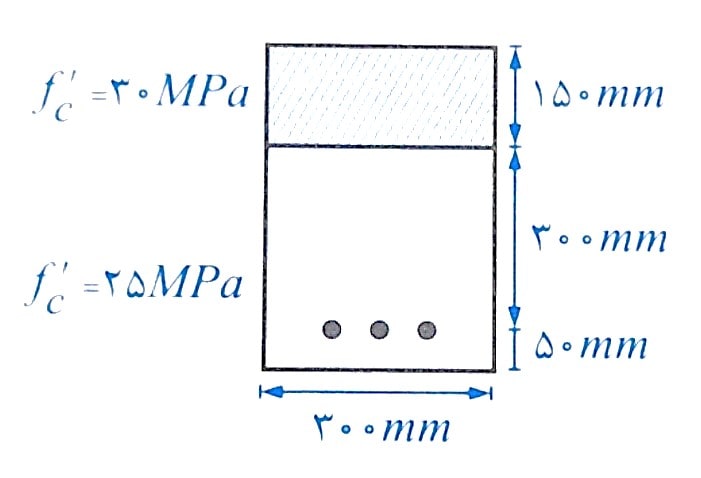
مثال: مقطع بتن آرمه ای به ابعاد 300×350 mm در نظر بگیرید.در این تیر برای تقویت مقاومت خمشی در ناحیه فوقانی مقطع به ضخامت 150 mm ، بتن فشاری 30 MPa اجرا شده است. افزایش لنگر خمشی اسمی مقطع در این حالت کدام است؟ (فولاد مقطع 3φ20 و فولاد از رده S400 است).

1)1.2 2)1.6 3)2 4)2.4

حل: برای درک بهتر سوال را با دو روش تحلیل می کنیم:

روش اول:

کافی است مقاومت خمشی اسمی مقطع در حالت اول و دوم را محاسبه کرده و سپس نسبت آنها را بدست آوریم. در حالت اول داریم:

در حالت دوم با فرض اینکه ناحیه فشاری مقطع در قسمت 150 میلی متری وجه فوقانی مقطع، یعنی در لایه با بتن جدید (f’_c=30 MPa) واقع می شود، ظرفیت خمشی مقطع را بدست می آوریم. فرض انجام شده را به راحتی می توانیم با محاسبه عمق بلوک فشاری کنترل نماییم:

بنابراین بلوک فشاری در ناحیه بتن با مقاومت فشاری 30 مگاپاسکال قرار داشته و فرض انجام شده صحیح است.

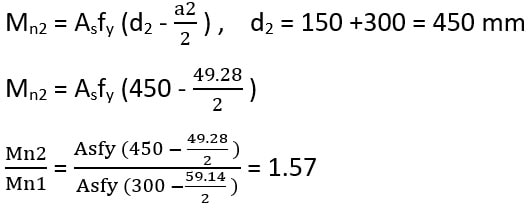
روش دوم: یک روش مفهومی است. در واقع باید به این نکته توجه کرد با اضافه کردن لایه 150 میلی متری بتن جدید، عمق موثر مقطع برابر 150+300=450 mm می شود که 1.5 برابر حالت اول d=300mm است.

بنابراین با توجه به تغییرات پارامترهای a و d مشخص است که در حالت جدید M_n کمی بیشتر از 1.5 برابر خواهد شد و با توجه به گزینه ها و بدون محاسبه نیز می توان گفت گزینه صحیح 2 است.

خمش دو محوره در تیرها

تیرها ممکن است در موارد خاص تحت خمش دو محوره یعنی وجود لنگر خمشی همزمان حول دو محور اصلی مقطع قرار گیرند. در حالت خمش دو محوره محور خنثی به صورت مورب و با زاویه نسبت به افق قرار می گیرد و مرکز بلوک تحت تنش فشاری یکنواخت نقطه C می باشد.

در تحلیل این موضوع می توان به موارد زیر اشاره کرد:

1- در این حالت با فرض جاری شدن میلگردها می توان نوشت:

2- در ادامه در صورتی که حول نقطه C (مرکز سطح بلوک فشاری معادل) در راستای قائم لنگر گیری شود، لنگر خمشی اسمی حول محور x بدست می آید:

M_nx = (A_s1f_y + A_s2f_y + A_s3f_y) e_y

همچنین در صورتی که حول C در راستای افق لنگر گیری شود، لنگر خمشی اسمی حول محور y بدست می آید:

M_ny = A_s1f_ye_x1 + A_s2f_ye_x2 + A_s3f_ye_x3

کنترل جاری شدن میلگردها، فرایند نسبتا دشوار و زمانبری دارد و برای مسائل آزمون نظام مهندسی مناسب نمی باشد. در سوال بعد این مفاهیم را بهتر درک می کنیم.

مثال: اگر تیر بتن مسلح شکل زیر با بتن درجا از رده C40 و فولاد رده S400 تحت اثر خمش دو محوره قرار بگیرد به طوری که محور خنثی به موازات قطر مقطع باشد، مقدار مولفه های لنگر خمشی اسمی مقاوم، حول محور x و حول محور y به ترتیب بر حسب kN.m به کدام مقادیر زیر نزدیک تر است؟ ( قطر آرماتور ها 20 میلی متر است و اندازه ها بر حسب میلی متر می باشد.)

1)65 و 17 2)33 و 17 3)65 و 33 4)33 و 33

حل: همانطور که در سوال گفته شده است، در صورتی که تیرهای بتن آرمه تحت لنگر خمشی در دو جهت واقع شود، محور خنثی به صورت زاویه دار نسبت به محورهای اصلی مقطع قرار می گیرد. در این حالت بدیهی است برای تحلیل مقاطع باید نمودار کرنش ها عمود بر این محور مورب رسم شده و تحلیل مقطع انجام شود. با توجه به اینکه در شکل محور خنثی مشخص شده است می توان لنگر خمشی مقاوم اسمی مقطع را از حالصلضرب نیروی کششی آرماتورها در بازوی آنها محاسبه کرد. برای این منظور ابتدا مساحت ناحیه فشاری تعادل با فرض جاری شدن میلگردها محاسبه می کنیم:

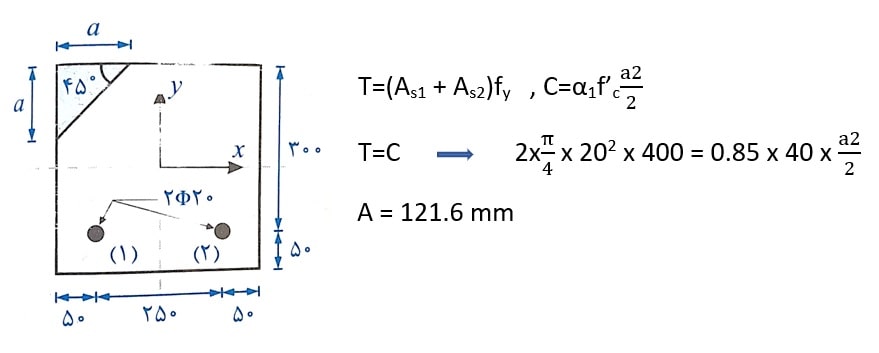
دقت شود که a بعد مثلثی است که تحت تنش فشاری 0.85f’_c قرار گرفته است. از طرفی قاعده مثلث بلوک فشاری معادل به موازات محور خنثی قرار داشته و زاویه 45 درجه با افق می سازد.

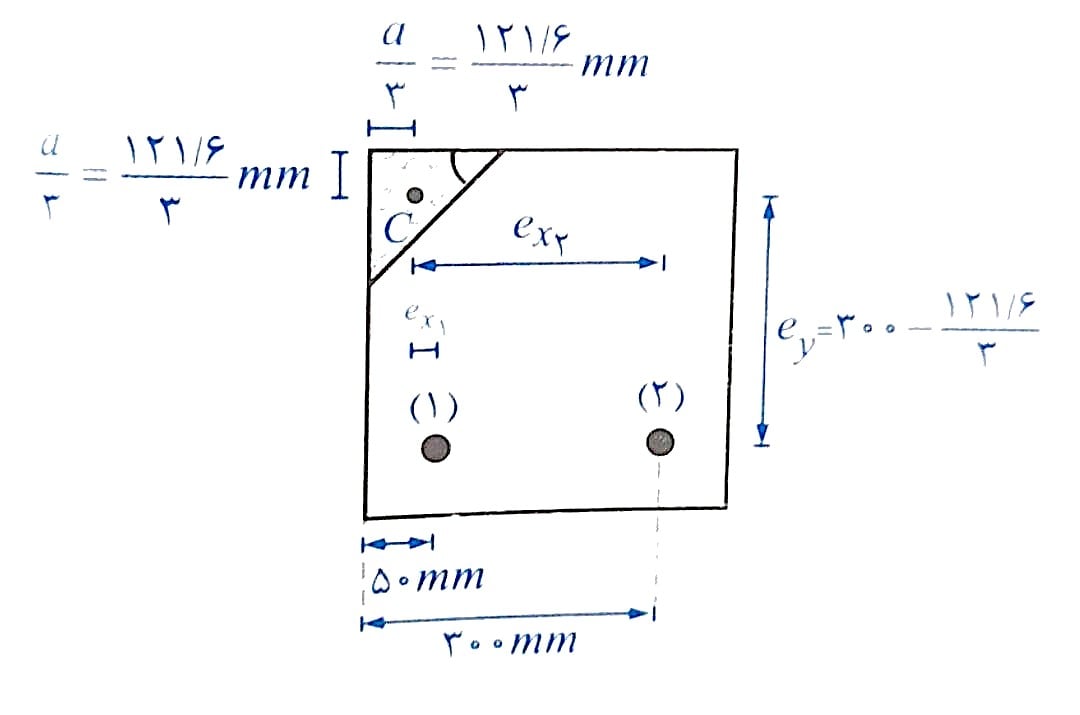
با توجه به اینکه مرکز سطح مثلث در فاصله 1/3 از قاعده واقع شده است. بنابراین لنگر خمشی اسمی حول محورهای x و y به صورت زیر محاسبه می شود. دقت شود که e_y فاصله مرکز سطح آرماتورها تا مرکز سطح مثلث در راستای y و e_x فاصله مرکز سطح هر آرماتور تا مرکز سطح مثلث در راستای x است.

شرح روش طرح مقاومت در کنترل خمش وارد بر مقطع

همانطور که می دانید هدف از طراحی یک مقطع بتن آرمه، تامین مقاومت مورد نیاز تحت بارهای نهایی وارد بر آن می باشد. این جمله بدان معنی است که در طراحی مقاطع بتن آرمه می خواهیم پس از اعمال بارهای مختلف وارد بر هر عضو، مقطع مطابق فرضیات در نظر گرفته شده و به نحوی باشد که از هر گونه شکست ناگهانی و پیشبینی نشده جلوگیری شود. در مبحث نهم ویرایش 99 این کنترل با رابطه زیر انجام می شود:

φ: ضریب کاهش مقاومت

S_n: مقاومت اسمی مقطع مورد نظر

Υ: ضریب افزایش باز

L: تلاش داخلی ناشی از بارها

در مورد اعضای خمشی رابطه فوق به صورت زیر بازنویسی می شود:

φM_n≥M_u

مثال: شکل زیر مقطع یک تیر بتن آرمه می باشد. در صورتی که بتن از رده C35 و فولاد هم S400 باشد، ضریب کاهش مقاومت خمشی را برای این تیر در لحظه نهایی تعیین کنید. آیا مقطع از نظر آیین نامه مجاز است؟

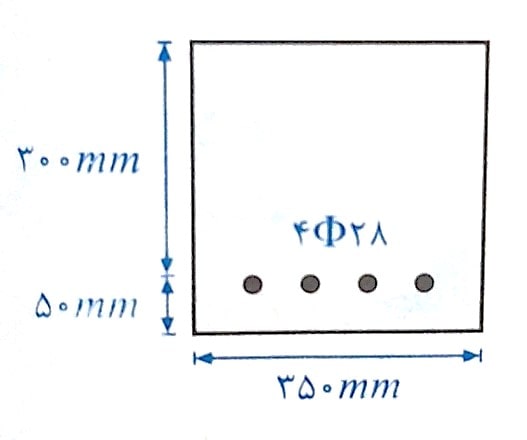
حل: همانطور که قبلا گفتیم مقدار ضریب کاهش مقاومت خمشی مقطع بر اساس عملکرد مقطع و مقدار کرنش فولادها در لحظه نهایی مشخص می شود. بنابراین باید مقدار کرنش فولاد ها را در لحظه نهایی با استفاده از رابطه تعادل و عمق محور خنثی بدست آوریم:

با توجه به کرنش فولاد و توضیحاتی قبلی A_smax<A_s≤A_sb قرار داشته و مقطع از نظر آیین نامه غیر مجاز است.

مثال: مقطع یک تیر بتن مسلح دارای عرض و ارتفاع موثر به ترتیب برابر 400 و 600 میلی متر است. در صورتی که بتن از رده C25 و فولاد مصرفی از آرماتور S400 باشد و آرماتورهای کششی مصرفی 4φ20 باشد، حداکثر مقدار لنگر خمشی قابل اعمال به این تیر حدودا چند کیلونیوتن متر می باشد؟

1)234 2)258 3)296 4)287

حل: در قدم اول برای محاسبه لنگر خمشی اسمی مقطع لازم است از روابط تعادل استفاده گردد.

محاسبه درصد آرماتور مورد نیاز مقطع

در طراحی تیرها با مشخص بودن طول تیر و بارگذاری اعمالی، لنگر طراحی مشخص بوده و معمولا لازم است درصد آرماتور مورد نیاز، بر اساس مشخصات مصالح مورد نظر و هندسه مقطع که معمولا بر اساس محدودیت های معماری و کنترل های بهره برداری بدست می آید محاسبه گردد. در بسیاری از سوالات آزمون نظام مهندسی نیر خواسته سوال تعیین درصد آرماتور مورد نیاز مقطع است که برای پاسخ به چنین سوالاتی راحت تر است از رابطه زیر استفاده کنیم:

تذکر: از جمله مهمترین کاربردهای رابطه فوق می توان به موارد زیر اشاره کرد:

هنگامی که محاسبه درصد آرماتور مورد نیاز مقطع تحت لنگر خمشی مشخصی مورد نیاز است. در این مورد نکته ای که بسیار حائز اهمیت است این است که در پایان محاسبات حتما مقدار درصد آرماتور محاسبه شده با مقادیر حداقل و حداکثر مجاز آیین نامه کنترل گردد.
هنگامی که حداقل ارتفاع مورد نیاز مقطع تحت لنگر مشخصی مورد سوال است.
هنگامی که می خواهیم مقاومت خمشی اسمی مقطع را براساس مشخصات آن به طور مستقیم و در یک مرحله بدست آوریم.

در ادامه با کنترل رابطه زیر و با توجه به مقادیر حداقل و حداکثر خواسته مساله بدست می آید:

برای درک بهتر این موضوع به حل چند مثال متنوع می پردازیم:

مثال: مقطع یک تیر خمشی بتن مسلح دارای عرض و ارتفاع موثر به ترتیب 400 و 655 میلی متر است. اگر بتن از رده C25 و آرماتورهای مصرفی از رده S340 و آرماتورهای کششی محاسباتی 4φ20 باشد، مقدار سطح مقطع آرماتور کششی لازم جهت تعبیه در مقطع به کدام یک از مقادیر زیر نزدیک تر است؟

1- 12.57 2- 10.74 3- 9.64 4- 16.72 میلی متر مربع

حل: به طور کلی هرگاه مقدار آرماتور مورد نیاز در سوال داده شد و آرماتورگذاری قابل قبول در مقطع مورد سوال قرار گرفت، مقدار آرماتور مورد نیاز را با مقادیر حداقل و حداکثر کنترل کنید. در این سوال با توجه به ابعاد نسبتا بزرگ مقطع و مقدار آرماتور داده شده، مشخصا مقدار حداقل ممکن است کنترل کننده باشد، آرماتور داده شده را با مقدار A_smin مقایسه می کنیم:

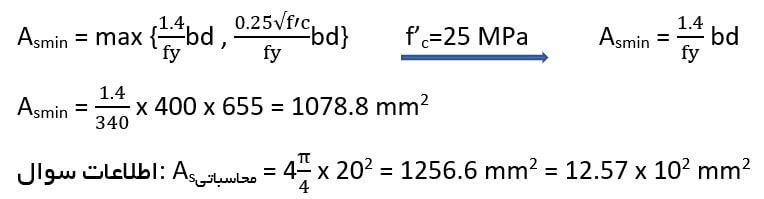
با توجه به بیشتر بودن A_s محاسباتی از A_smin بنابراین مساحت آرماتور لازم برای تعبیه در مقطع برابر 12.57 x 10² mm² بوده و گزینه 1 صحیح است.

مثال: در صورتی که لنگر حداکثر وارد بر مقطع تیر زیر برابر M_u = 40 kN.m باشد، مقدار آرماتور کششی مورد نیاز مقطع به کدامیک از مقادیر زیر نزدیک تر است؟ (f’_c=22.5 Mpa و fy=400 MPa)

1- 4.8 2- 3.4 3- 4.5 4- 5.2 (سانتی متر مربع)

مثال: یک مقطع بتن آرمه با ابعاد b=300 mm و d=400 mm و دارای چهار عدد میلگرد φ20 از رده S400 در ناحیه کششی است. چنانچه نوع بتن مقطع از C25 به C50 تغییر یابد، لنگر خمشی مقاوم اسمی تیر حدودا چند درصد افزایش می یابد؟

1)5 2)12 3)20 4)30

حل: با تغییر مقاومت فشاری بتن، عمق بلوک فشاری و در نتیجه مقدار بازوی لنگر تغییر می یابد دراین صورت داریم:

دقت شود در صورت استفاده از بتن رده C50 مقدار α₁=0.85 ثابت و برابر 0.85 می باشد.

با توجه به ثابت بودن مساحت آرماتورهای کششی در هر دو حالت نسبت به لنگر خمشی اسمی برابر نسبت بازوی لنگر در هر دو حالت خواهد بود. بنابراین داریم:

روش مفهومی و سریع

در مقاطعی که بر اساس آیین نامه طراحی شده و شکست نرم دارند، افزایش مقاومت فشاری بتن بین5 تا 10 درصد بر روی ظرفیت خمشی اثر می گذارد. با توجه به این نکته میشد بدون حل سوال پاسخ صحیح را بدست آورد.

مثال: شکل زیر یک تیر طره را نشان می دهد که تحت بار مرده q_D=w و بار زنده q_L=0.5w بر حسب kN/m قرار گرفته است. در صورتی که عرض تیر برابر 300 mm، عمق موثر 400 mm آرماتورهای کششی 3φ20 و مصالح مصرفی C25 و S400 باشد، به موارد زیر پاسخ دهید.

الف) در لحظه نهایی محور خنثی در چه فاصله ای از تار فوقانی تیر قرار می گیرد؟

ب)کرنش آرماتورهای کششی در لحظه نهایی چقدر است؟

ج) حداکثر مقدار w چقدر باید باشد تا تیر در آستانه گسیختگی قرار بگیرد؟

حل:

الف) در لحظه نهایی کرنش در دورترین تار فشاری بتن برابر 0.003 می باشد، اما به دلیل مشخص نبودن مقدار کرنش آرماتور کششی و همچنین محل محور خنثی، نمی توان در این مرحله از نمودار کرنش ها استفاده کرد و باید ابتدا با استفاده از رابطه تعادل، عمق بلوک فشاری را تعیین کنیم. دقت شود با توجه به اینکه در تیرهای طره تحت بار ثقلی، لنگر منفی اتفاق می افتد ناحیه فشاری در این تیر در قسمت تحتانی مقطع می باشد.

در سوال فاصله محور خنثی تا تار خواسته شده، بنابراین با توجه به اینکه ناحیه فوقانی، ناحیه کششی مقطع است، بنابراین خواسته مساله مقدار h-x می باشد.

h-x=450-69.5=380.5 mm

ب) با توجه به مشخص شدن مقدار x می توانیم نمودار کرنش ها را رسم کنیم و مقدار Ԑ_s را بدست آوریم:

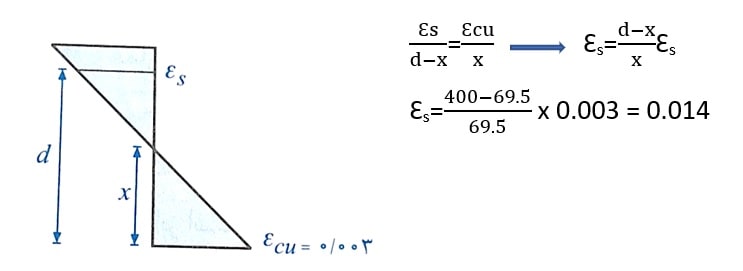
دقت شود که از مقدار Ԑ_s مشخص است که تیر در محدوده کشش-کنترل قرار داشته و ضریب φ برای آن 0.9 است.

Ԑ_s=0.014>Ԑ_y+0.003=0.005

ج) اگر بخواهیم تیر در آستانه گسیختگی قرار بگیرد باید بار وارده برابر بیشترین مقدار ظرفیت تیر گردد. با توجه به اینکه در سوال بارهای مرده و زنده به طور مجزا ارائه شده است، بنابراین باید مطابق ترکیب بار آیین نامه که با در نظر گرفتن ترکیب بارهای بحرانی می باشد به صورت زیر بنویسیم:

q_u=1.2q_D+1.6q_L

q_u=1.2w+1.6×0.5w = 2w

از طرفی حداکثر لنگر خمشی ناشی از بار خطی در این تیر طره برابر است با:

مثال: به یک مقطع بتن آرمه با ابعاد نشان داده شده در شکل زیر بر حسب میلی متر، لنگرهای خمشی M_D=50 nN.m و M_L=30 kN.m اعمال می شود. در صورتی که مصالح مصرفی بتن رده C25 و فولاد رده S400 باشد. کدامیک از گزینه های زیر را می توان به عنوان آرماتورهای مورد نیاز تیر در مقطع به کار برد؟

3φ25 3φ16 3φ20 3φ18

حل: همانطور که در تمرین های قبلی دیدیم وقتی که بارهای وارده به صورت مجزا داده شده اند برای محاسبه بار نهایی باید از ترکیب بار استفاده کنیم. در این سوال چون لنگرهای مرده و زنده داده شده اند باید لنگرنهایی را محاسبه کنیم:

M_u=1.2M_D+1.6M_L

M_u=1.2×50+1.6×30 = 108 kN.m

می دانیم طراحی مقطع باید طوری باشد که φM_n≥M_u باشد بنابراین:

0.9M_n≥108 M_n≥120 kN.m

برای تعیین مقدارآرماتور محاسباتی تیر با استفاده از رابطه ساده شده مقاومت خمشی اسمی داریم:

مثال: تیر بتنی با مقطع مستطیلی با دهانه 6 متری و تکیه گاه ساده تحت بارگذاری گسترده یکنواخت ضریبدار q_u=55 kN/m قرار دارد. به سبب محدودیت های معماری ارتفاع تیر باید دارای کمترین مقدار باشد. برای این منظور به لحاظ مقاومتی و بدون توجه به حضور آرماتورهای فشاری در مقطع، ارتفاع تیر در حالتی که عرض آن برابر 400 mm باشد، به کدامیک از مقادیر زیر نزدیک تر است؟ از وزن واحد طول تیر صرف نظر شود. (f_y=400 Mpa , f_c’=25 Mpa)

H=455 H=410 H=368 H=338

حل: لنگر ضریبدار وارده بر تیر برابر است با:

همانطور که می دانید، ظرفیت خمشی مقطع با توجه به لنگر اعمالی از رابطه زیر بدست می آید:

با توجه به اینکه میزان آرماتور مقطع تیر داده نشده است و کمترین مقدار ممکن برای d خواسته شده است، پس هرچقدر درصد آرماتور (ρ) افزایش یابد، مقدار d کاهش می یابد. بنابراین باید حداکثر درصد آرماتور طولی را برای این تیر در نظر بگیریم تا d ودر نهایت ارتفاع تیر حداقل شود، در این صورت داریم: