طراحی ستون های لاغر

طراحی ستون های لاغر

محاسبه ضریب لاغری ستون ها

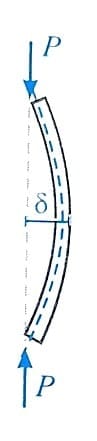
ستونی مطابق شکل زیر را در نظر بگیرید که تحت اثر بار محوری P و نیروی جانبی Q قرار دارد. تحت این نیروی جانبی، تغییر شکل جانبی ∆ در انتهای آزاد ستون ایجاد می گردد.

با توجه به وجود بار جانبی، در تکیه گاه ستون لنگر QL ایجاد شده و از طرفی تحت اثر بار جانبی، اختلاف تغییر مکانی به اندازه ∆ بین انتهای فوقانی و تحتانی  ستون به وجود آمده است و در اثر این موضوع، لنگر خمشی دیگری نیز در اثر خروج از مرکزیت ایجاد شده برای بار P به وجود می آید که مقدار آن برابر P∆ می باشد.

در این صورت مقدار کل لنگر ایجاد شده در تکیه گاه را می توان به صورت زیر بدست آورد:

باید توجه شود که لنگر ثانویه P∆ باعث افزایش لنگر کل ستون و در نتیجه افزایش تغییر شکل های جانبی شده و افزایش تغییر شکل نیز مجددا باعث ایجاد لنگر ثانویه می گردد و در صورتی که اثر افزایش لنگر خمشی در طراحی ستون لحاظ نشده باشد، طراحی ستون نادرست بوده و لنگر خمشی وارد ه به صورت صحیح برآورد نشده است.

با توجه به رابطه فوق، ارتباط لنگر وارد بر ستون با نیروی P، به صورت غیر خطی است. در واقع هر چه قدر مقدار P افزایش یابد، مقدار لنگر ستون و در نتیجه تغییر شکل ایجاد شده در ستون یعنی پارامتر ∆ افزایش یافته و این موضوع یعنی ارتباط M و P (به دلیل حضور پارامتر ∆) خطی نبوده و به این اثر در اصطلاح اثر غیر خطی هندسی می گویند.

با توجه به تاثیر مستقیم اثر افزایش لنگر مذکور در نتایج طراحی ستون ها، بحث لنگر ثانویه  از بحث های مهم در مهندسی عمران محسوب می شود و اصطلاحا آن را اثر P-∆ می نامند. با یک نگاه دقیقتر می توان گفت که اثر P-∆ به نوعی باعث کاهش ظرفیت ستون می شود.

نکته: اثر P-∆ فقط مربوط به ستون های مهار نشده ای که دارای تغییر مکان جانبی نسبت به تکیه گاه هستند نبوده و در ستون های مهار شده ای که در آنها تغییر مکان جانبی δ مطابق شکل بین دو انتهای ستون رخ می دهد نیز تعریف می گردد.

ستون های کوتاه: در این ستون ها با در نظر گرفتن لنگر ثانویه، میزان کاهش در مقاومت ستون کمتر از 5 درصد بوده و لذا می توان از اثرات آن صرف نظر کرد، در این خصوص طراحی ستون بدون در نظر گرفتن پارامترهای خاص و مطابق آنچه در فصل ششم گفته شده انجام می شود.

ستون های لاغر: در این ستون ها، اثر لنگر ثانویه قابل صرف نظر کردن نبوده و باید به طور دقیق در طراحی لحاظ شود.

بر این اساس برای هر ستون پارامتری به نام نسبت لاغری تعریف شده که با λ نمایش داده می شود. در واقع λ پارامتری است که حساسیت ستون نسبت به پدیده کمانش و اثر P-∆ را نشان می دهد.

هر چه مقدار این ضریب بزرگتر باشد، پدیده کمانش و اثر P-∆ نیز بیشتر در ستون تاثیر می گذارد.

برای بررسی اثر لنگرهای ثانویه در ستون های لاغر می توان از دو روش زیر استفاده کرد:

1)تحلیل دقیق کامپیوتری: در این روش از نرم افزاری مانند SAP2000 یا ETABS که امکان تحلیل مرتبه دوم داشته و لنگرهای ثانویه را در طراحی لحاظ می کند استفاده می شود.

2)تحلیل با ضریب تشدید لنگر: این روش یکی از ابتکارات مهندسین عمران برای ساده سازی طراحی ستون های لاغر بوده و مبنای آن استفاده از ضریب تشدید لنگر است.

در این روش با استفاده از روابطی خاص ضریبی افزاینده (بزرگتر از یک) به عنوان ضریب تشدید لنگر محاسبه شده و با ضرب آن در مقدار لنگرهای استاتیکی اولیه، لنگرهای ثانویه یا تشدید یافته محاسبه می شوند، در نهایت طراحی ستون بر مبنای این مقادیر انجام می گردد.

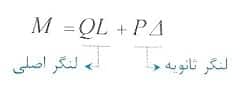
بیشتر بدانیم

در شکل های زیر لنگر ایجاد شده در اثر خروج از مرکزیت نیرو در ستون برابر Pe است. اگر تغییر شکل ∆ در وسط ارتفاع ستون در اثر لنگرهای انتهایی Pe ایجاد گردد، لنگر در این مقطع به اندازه P∆ افزوده شده و به P(e+∆) می رسد. حال فرض کنید می خواهیم با افزایش نیروی P ستون گسیخته شود.

اگر نسبت لاغری ستون به حدی باشد که ستون لاغر محسوب شود (مثلا به دلیل طول زیاد ستون)، رابطه P و M وارد بر ستون غیر خطی خواهد شد. برای درک بهتر این موضوع به شکل زیر که مسیر رسیدن ستون در دو حالت کوتاه و لاغر به حالت گسیختگی را با افزایش نیروی P نمایش می دهد، توجه کنید.

ستون کوتاه: M=Pe         (A(نقطه

ستون لاغر: M=P(e+∆)   (Bنقطه )

در ستون لاغر مسیر بارگذاری از P=0 تا لحظه نظیر گسیختگی مقطع یک منحنی شده و هنگامی که این منحنی با منحنی اندرکنش برخورد کند (نقطه B) ستون گسیخته می شود.

در این حالت اگرچه مقطع ستون و خروج از مرکزیت بار تغییر نکرده  است، اما لاغری ستون به دلیل طول زیاد آن سبب کاهش مقاومت محوری ستون از مقدار P_A به P_B و همچنین افزایش لنگر خمشی از M_A به M_B در لحظه نهایی شده است.

در این حالت شکست ستون به دلیل شکست مصالح ایجاد شده است. این نوع شکست، در ستون های کوتاه و لاغر می تواند رخ دهد.

اگر نسبت لاغری ستون خیلی زیاد باشد، بارگذاری آنقدر غیرخطی می شود که قبل از رسیدن به منحنی اندرکنش و رسیدن کرنش دورترین تارفشاری بتن به کرنش Ԑ_cu ستون دچار ناپایداری و کمانش می شود.

در این حالت قبل از اینکه  بتن در وجه فشاری خرد شده و خرابی ستون اتفاق بیفتد، به دلیل لاغری بیش از حد، ستون کمانش می کند (مانند منحنی ستون C).

محاسبه ضریب لاغری

همانطور که گفته شد، برای تعیین وضعیت لاغری ستون ها از ضریب لاغری (λ) استفاده می شود که مقدار آن براساس رابطه زیر بدست می آید:

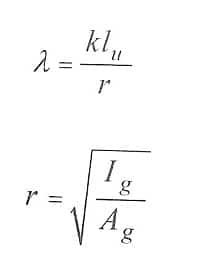
K:ضریب طول موثر ستون

L_u: طول آزاد یا مهار نشده ستون میلی متر

I_g: ممان اینرسی ناخالص مقطع حول مرکز ثقل بدون در نظر گرفتن آرماتورها

A_g: مساحت ناخالص مقطع

r: شعاع ژیراسیون مقطع

مقدار شعاع ژیراسیون مقاطع مستطیلی و دایروی را می توان به صورت ساده تر و با استفاده از روابط زیر محاسبه نمود.

1)در ستون های با مقطع مستطیل در هر امتداد برابر 0.3 بعد ستون در آن امتداد.

b و h: عرض و عمق مقطع مستطیلی

2)در ستون ها با مقطع دایره برابر با 0.25 قطر مقطع ستون.

r=0.25D

تعیین وضعیت مهار جانبی ستون ها

هنگامی که تغییر مکان جانبی ابتدا و انتهای ستون یا طبقه ناچیز باشد، ستون یا طبقه زیر به لحاظ جانبی، مهار شده تلقی می گردد، در غیر این صورت ستون و یا طبقه مورد نظر مهار جانبی نشده در نظر گرفته می شود. مطابق آیین نامه در مواردی که یکی از دو شرط زیر برقرار باشد، ستون ها و طبقات سازه را می توان مهار شده در نظر گرفت:

1)افزایش لنگرهای انتهایی ستون ها در اثر تحلیل مرتبه دوم، از 5 درصد لنگرهای انتهایی ستون ها در تحلیل مرتبه اول بیشتر نباشد.

2)شاخص پایداری طبقه که از رابطه زیر محاسبه می شود، از 0.05 بیشتر نباشد.

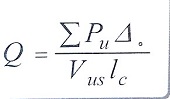
ΣP_U: مجموع بارهای قائم ضریبدار در طبقه که متناظر با آن حالت بار جانبی است که در آن مقدار مجموع بارهای قائم طبقه حداکثر باشد، نیوتن.

∆₀: تغییر مکان جانبی نسبی مرتبه اول دو انتهای ستون در طبقه مورد نظر تحت اثر نیروی برش V_US  میلی متر

V_us: نیروی برشی طبقه، نیوتن.

L_c: طول ستون که برابر فاصله مرکز تا مرکز ناحیه اتصال تیر به ستون در نظر گرفته می شود. میلی متر.

نحوه محاسبه ضریب طول موثر ستون

طول موثر ستون از لحاظ مفهومی، نشان دهنده فاصله بین نقاط عطف منحنی تغییر شکل ستون بوده و از حاصلضرب ضریب طول موثر در کل ستون بدست می آید. از جمله پارامترهای تاثیر گذار در مقدار این ضریب، وضعیت مهار جانبی، سختی خمشی مقطع و مشخصات تیرها و ستون های منتهی به گره های فوقانی و تحتانی ستون و همچنین طول اعضا می باشد.

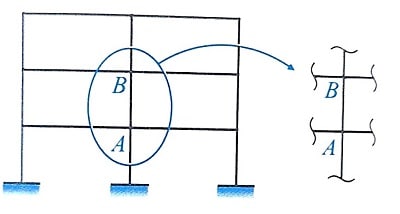
به منظور تعیین مقدار این ضریب برای ستون AB در شکل مقابل، پس از تعیین وضعیت مهار جانبی قاب، کافیست گام های زیر طی شود:

گام اول: ضریب Ψ که برابر نسبت سختی خمشی موثر ستون به تیرهای منتهی به گره در محل اتصال است، برای گره های فوقانی و تحتانی که معادل تکیه گاه های فوقانی و تحتانی ستون هستند، با توجه به اصلاحیه مبحث نهم مقررات ملی ساختمان مطابق رابطه زیر محاسبه می شود:

Ψ: نسبت سختی خمشی ستون به تیر در محل گره مورد نظر

EI: سختی خمشی عضو

l_c: طول ستون یا تیر که برابر فاصله مرکز تا مرکز تکیه گاه ها می باشد.

گام دوم: با توجه به وضعیت مهارشدگی جانبی ستون و براساس مقادیر Ψ_A و Ψ_B بدست آمده از مرحله قبل، مقدار ضریب طول موثر مطابق نموگرام های زیر تعیین می شود.دقت نمایید برای این هدف کافیست مقدار Ψ_A و Ψ_B را بر روی هر ستون از نموگرام مشخص کرده و آنها را توسط خطی به هم متصل نمایید. عدد متناظر با محل تقاطع این خط با ستون میانی بر روی نموگرام که با k مشخص شده است، بیانگر مقدار ضریب طول موثر خواهد بود.

تذکر مهم: ضریب Ψ از لحاظ مفهومی قابلیت دوران گره را نشان می دهد. از لحاظ تئوری در تکیه گاه های مفصلی این ضریب برابر بی نهایت و در تکیه گاه های گیردار برابر صفر است. در ویرایش های قبلی مبحث نهم مقررات ملی ساختمان ضریب Ψ برای تکیه گاه های مفصلی برابر 10 در نظر گرفته می شد. این موضوع در ویرایش 99 مقررات ملی ساختمان آورده نشده است.

محاسبه مقدار سختی عضو

به منظور محاسبه مقدار سختی عضو (EI)، باید اثر ترک خوردگی اعضا در نظر گرفته شود. برای این منظور با توجه به توضیحات فصل اول می توان از دو روش ساده و دقیق ممان اینرسی اعضای مختلف را محاسبه کرد. مقادیر ممان اینرسی اعضا در روش تقریبی مطابق جدول زیر می باشد.

در جدول فوق I_g مقدار ممان اینرسی مقطع بدون در نظرگرفتن آرماتورها است.

اما در صورتی که مقدار ممان اینرسی اعضای مختلف به صورت دقیق تری مورد نظر باشد از جدول زیر استفاده می شود.

در اعضای خمشی ممتد به منظور محاسبه مقدار I می توان مقدار متوسط آن را در مقاطع با لنگرهای خمشی مثبت و منفی بحرانی در نظر گرفت. همچنین در محاسبه مقادیر P_u و M_u باید از ترکیب بار مورد نظر در محاسبات و یا ترکیبی که کمترین مقدار I را نتیجه می دهد استفاده نمود.

تذکر 1: در صورت وجود بارهای جانبی دائمی، لازم است مقادیر ممان اینرسی اعضای قائم از جمله ستون و دیوارها بر ضریب 1+β_ds تقسیم گردند. ضریب β_ds که ضریب تاثیر اثر خیزش و نیروهای دائمی می باشد. به صورت زیر محاسبه می شود:

دقت شود هر دو عبارت صورت و مخرج کسر فوق متعلق به یک ترکیب بار می باشند.

تذکر 2: از لحاظ مفهومی پارامتر β_ds برای یک قاب با حرکت جانبی نزدیک به صفر است، زیرا بارهای جانبی مانند زلزله معمولا دارای اثر کوتاه مدت هستند. β_ds مخالف صفر، زمانی رخ می دهد که به عنوان مثال ساختمان تنها از یک سمت تحت فشار جانبی خاک قرار بگیرد.

تذکر 3: در خصوص تیرهای T شکل مقدار ممان اینرسی ناخالص (I_g) باید با محاسبه عرض موثر بال انجام شود، به طور تقریبی می توان مقدار ممان اینرسی این مقطع را دو برابر ممان اینرسی مقطع مستطیلی جان (با صرف نظر از قسمت بال ها) لحاظ نمود.

تذکر 4: در تحلیل اعضا تحت بارهای جانبی ضریبدار، می توان ممان اینرسی تمام اعضا را برابر 0.5 I_g در نظر گرفت.

تذکر 5: در تحلیل دال های دو طرف بدون تیر که جزئی از سیستم باربر جانبی زلزله در نظر گرفته می شوند، مقادیر ممان اینرسی I برای دال ها براساس مدلی که با نتایج آزمایش ها و تحلیل ها مطابقت قابل قبولی داشته باشد بدست می آید.

مثال: شکل زیر مقطع یک ستون بتن آرمه با ارتفاع 4 متر نشان می دهد. در صورتی که ضریب طول موثر در این ستون در کمانش حول محورهای x و y به ترتیب برابر 1.4 و 1.8 باشد، ضریب لاغری حول کدام محور ستون می تواند اثر بیشتری در طراحی داشته باشد؟ ابعاد بر حسب میلی متر می باشد.

حل: مطابق خواسته سوال، ضریب لاغری حول هر دو محور خواسته شده است. باید توجه شود در چنین حالتی باید مقادیر ضریب طول موثر (k) و شعاع ژیراسیون (r) به نحو صحیحی در هر دو راستا محاسبه شوند. با توجه به این موضوع داریم:

دقت شود در محاسبه مقدار شعاع ژیراسیون از  رابطه دقیق استفاده شده و همچنین در محاسبه ممان اینرسی حول محور مورد نظر، بعدی که عمود بر محور خمش بوده، توان 3 دارد (بعد خمشی).

با توجه به بیشتر بودن مقدار λ_x نسبت به λ_y، بنابراین لاغری حول محور x اثر بحرانی تری در طراحی ستون دارد.

تذکر 1: چنانچه محاسبه شعاع ژیراسیون به طور تقریبی مد نظر باشد، کافی است بعد خمشی در هر راستا به طور صحیح انتخاب گردد.

روابط تقریبی: r_x=0.3×300=90 mm , r_y=0.3×600=180 mm

تذکر2: با توجه به اختلاف جزئی بین مقادیر r حاصل از رابطه دقیق و تقریبی، معمولا در سوالات آزمون نظام مهندسی از روش تقریبی استفاده شده که البته در اغلب اوقات این موضوع در صورت سوال نیز ذکر می شود.

مثال: در یک ستون بتن آرمه مقادیر Ψ_A و Ψ_B در چند حالت مطابق جدول زیر، در دو وضعیت مهار جانبی شده و مهار جانبی نشده ارائه شده است. مقدار ضریب طول موثر متناظر با هر حالت را بدست آورید.

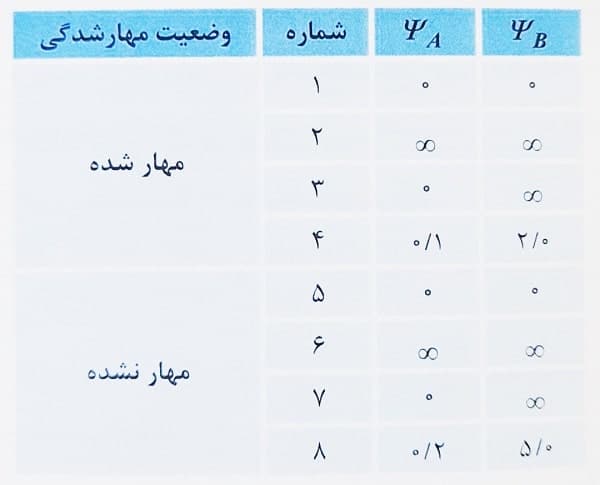
حل: حالت 1 و 5: در حالت اول ستون مهار شده بوده و Ψ_A=Ψ_B=0 می باشد. با توجه به رابطه ضریب طول موثر ستون، این موضوع از لحاظ ریاضی یعنی سختی ستون ها ناچیز بوده و به عبارت دقیق تر می توان گفت که سختی تیر در برابر سختی ستون بسیار قابل توجه می باشد.

در واقع در این حالت، نقاط A و B مشابه تکیه گاه گیردار عمل کرده و می توان ستون را به صورت مقابل مدل کرد.

با توجه به نموگرام و مشخص کردن Ψ_A و Ψ_B از نقطه صفر، مقدار k=1 بدست می آید.

حالت 2 و 4: در حالت دوم هر دو مقدار Ψ برابر بی نهایت در نظر گرفته شده اند. این حالت معرف شرایطی است که سختی تیر ناحیه اتصال بسیار ناچیز بوده و در واقع شرایط تکیه گاه مفصلی را بیان می کند.

بنابراین ستون را در این حالت می توان به صورت زیر در نظر گرفت. در حالت مهار شده، با مشخص نمودن دو نقطه Ψ_A و Ψ_B بر روی نمودار، خط افقی بدست می آید که خط نمودار k را در نقطه 1 قطع می کند.

بنابراین در حالت مهار شده، مقدار K در این شرایط برابر 1 می باشد.

در حالت مهار نشده به طور متناظر مقدار k برابر ∞ بدست می آید. باید توجه نمود که در حالت مهار نشده جانبی، ستون با دو تکیه گاه مفصلی مطابق شکل بالا، ناپایدار تلقی شده و k=∞ نیز بر همین مفهوم دلالت می کند.

بنابراین این حالت به صورت تئوری تعریف شده و در عمل لازم است مقدار Ψ در کی از تکیه گاه ها از طریق تعبیه تکیه گاه های جانبی و یا تعبیه تیرهای مناسب، کاهش داده شود.

حالت 3 و 7: در حالتی که یک انتها دارای Ψ_A=0 و انتهای دیگر Ψ_B=∞ است، در واقع مدل ستون ترکیبی از دو حالت گفته شده فوق یعنی یک طرف با تکیه گاه مفصلی و طرف دیگر با تکیه گاه گیردار در نظر گرفته می شود.

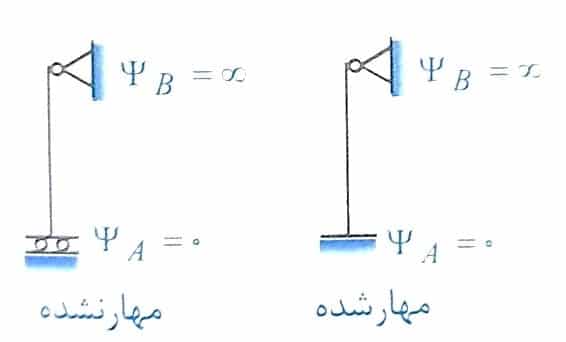
در حالت مهار شده با مشخص نمودن مقدار Ψ در هر سمت نموگرام، خط بدست آمده محور k را در نقطه 0.7 قطع می نماید، لذا در حالت مهار شده k=0.7 می باشد. در حالت مهار نشده نیز با استفاده از نموگرام مربوطه، k=2 بدست می آید.

حالت 4: در حالتی که Ψ_A=1 و Ψ_B=2 می باشد، در شرایط مهار شده، خط اتصال این دو نقطه محور k را در نقطه حدود 0.68 قطع می کند.

حالت 8: در صورتی که Ψ_A=2 و Ψ_B=5 باشد، در شرایط مهار نشده، با اتصال خط واسط بین نقاط مذکور، مقدار k حدود 1.58 بدست می آید.

تذکر: نتایج بدست آمده مطابق حالت مرزی 1 تا 3 این تمرین، به راحتی و با استفاده از نمودار تغییر شکل جانبی ستون ها مطابق مفاهیم درس مقاومت مصالح قابل محاسبه است.

مثال: ضریب طول موثر ستون AB در قاب مهار نشده بتنی با تکیه گاه های گیردار مطابق شکل، در صورتی که Ψ_A=1 باشد، به کدامیک از اعداد زیر نزدیک تر است؟ (ضریب Ψ برای تکیه گاه B را صفر در نظر بگیرید)

1)1.35                  2) 1.17                       3)1.93                         4)2.35

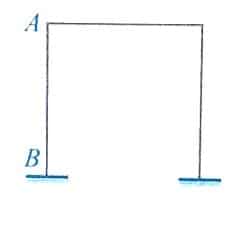
حل: با توجه به نموگرام محاسبه ضریب طول موثر در ستون های مهار نشده و با اتصال دو نقطه Ψ_A=1 و Ψ_B=0 به طور تقریبی مقدار k=1.17 بدست می آید بنابراین گزینه 2 صحیح است.

مثال: در یک قاب بتن آرمه که فاقد مهار جانبی می باشد، در صورتی که ابعاد مقطع تمام ستون ها 400 در 400 میلی متر و تمام تیرها 400 در 600 میلی متر است، ضریب طول موثر ستون AB در صفحه قاب به کدامیک از مقادیر زیر نزدیکتر است؟ قاب مهارنشده فرض شود و استفاده از نتایج تحلیل دقیق مدنظر نیست. وزن مخصوص بتن برابر 250 کیلوگرم بر متر مکعب فرض شده و 40 درصد برش ستون ها، حاصل از بارهای دائمی ناشی از فشار خاک است. بتن از رده C30 می باشد. از اثر خزش در تیرها صرف نظر شود.

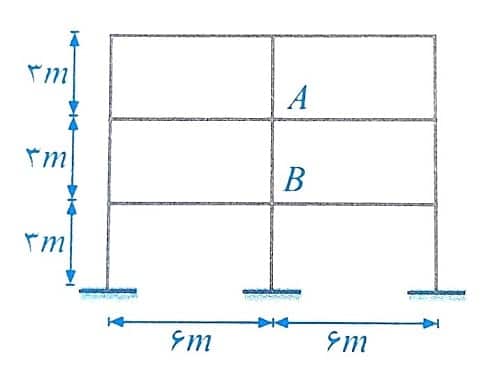
1)1.28                          2)1.10                             3)1.42                      4)1.33

حل: برای محاسبه ضریب طول موثر، لازم است مقادیر Ψ_A و Ψ_B در دو انتهای ستون محاسبه گردد. در این صورت با توجه به تعریف Ψ و رابطه گفته شده داریم:

با توجه به اینکه 40 درصد برش ستون AB حاصل از بارهای دائمی است، بنابراین β_ds=0.4 می باشد. با توجه به ابعاد مشخص شده برای اعضا و جدول بالا داریم:

با توجه به اینکه هر دو گره A و B به دو ستون و دو تیر ختم می شوند، بنابراین برای محاسبه نسبت Ψ به صورت زیر عمل می کنیم:

با توجه به یکسان بودن شرایط گره های A و B داریم:

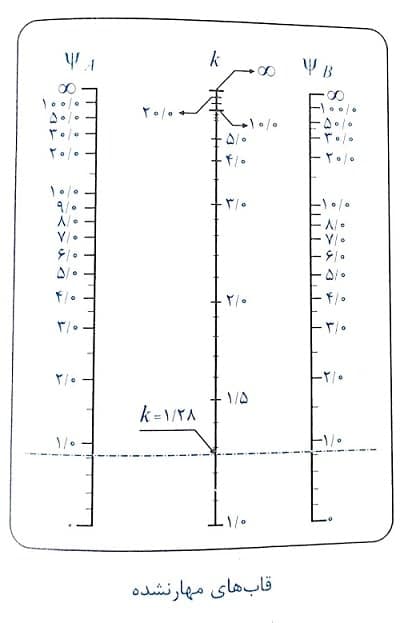
در این صورت با توجه نموگرام ستون های مهار نشده، به طور تقریبی مقدار k=1.28 بدست می آید و گزینه 1 صحیح می باشد.

صرف نظر از اثر لاغری

ممکن است ضریب لاغری بدست آمده بسیار کوچک باشد، در این صورت می توان از اثر لاغری در طراحی ستون صرف نظر کرد و طراحی را مطابق ضوابط ستون های کوتاه انجام داد. در این خصوص دو حالت زیر در نظر گرفته می شود:

1)در ستون های مهار نشده، در صورتی که kl_u/r≤22 باشد، می توان از اثر لاغری در طراحی ستون صرف نظر کرد.

2)در ستون های مهار شده، اگر ضریب لاغری در نامساوی زیر صدق نماید، می توان از اثر لاغری در طراحی ستون صرف نظر نمود:

در رابطه بالا M₁ و M₂ به ترتیب لنگرهای خمشی دو انتهای ستون بوده، به طوری که M₁ از نظر مقداری کوچکتر از M₂ است، یعنی در حالت کلی 1>│M₁/M₂│ بوده و با توجه به جهت آنها، اگر انحنای ستون در یک جهت باشد، این کسر منفی و اگر ستون دارای انحنا در دو جهت باشد، این کسر مثبت خواهد بود.

نکته: در صورتی که ستون تحت بار جانبی در فاصله بین تکیه گاه ها باشد، مقدار M₂ برابر بزرگترین لنگر وارده بر ستون در نظر گرفته می شود.

در ادامه به بررسی چندین سوال متنوع از این بحث مهم و پر تکرار در آزمون نظام مهندسی می پردازیم.

مثال: در یک قطعه فشاری بتن مسلح مهار شده در صورتی که k=1 و طول آزاد عضو 5 متر و ابعاد مقطع 400 در 400 باشد و لنگرهای خمشی موثر در دو انتهای عضو 60 و 80 کیلو نیوتن متر و این لنگرها موجب انحنای ستون در دو جهت شوند، گزینه صحیح را انتخاب کنید. شعاع ژیراسیون مقطع برابر 0.3 بعد کلی مقطع در نظر گرفته شود).

1)چون انحنای ستون در دو جهت است، می توان از اثر لاغری صرف نظر کرد.

2)چون مقدارk برابر واحد است، می توان از اثر لاغری صرف نظر کرد.

3)نمی توان از اثر لاغری صرف نظر کرد.

4)چون لنگرهای خمشی دو انتهای ستون هم علامت هستند می توان از اثر لاغری صرف نظر کرد.

حل: با استفاده از مشخصات ارائه شده، مقدار ضریب لاغری ستون به صورت زیر محاسبه می شود:

با توجه به اینکه ستون مهار شده بود و انحنای ستون در دو جهت رخ می دهد داریم:

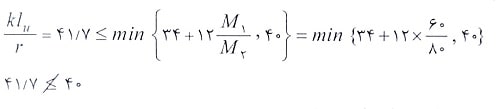
با توجه به بیشتر بودن مقدار ضریب لاغری از مقدار 40، بنابراین نمی توان از اثر لاغری در طراحی ستون صرف نظر کرد و گزینه 3 صحیح است.

مثال: برای یک ستون مهار شده بتن مسلح با مقطع 400×400 میلی متر و ضریب طول موثر واحد با طول آزاد سه متر، حداکثر نسبت لنگر خمشی نهایی کوچکتر به لنگر خمشی نهایی بزرگتر در دو انتهای ستون M₁/M₂ به کدامیک از گزینه های زیر نزدیکتر باشد تا بتوان از اثر لاغری صرف نظر کرد؟ شعاع ژیراسیون مقطع به صورت دقیق محاسبه گردد. انحنای ستون در یک جهت فرض شود.

1)1                         2)0.65                      3)0.7                        4)0.5

حل: با توجه به اینکه ستون مهار شده است داریم:

با توجه به اینکه می دانیم انحنای ستون در یک جهت است، بنابراین نسبت M₁/M₂ منفی بوده و به همین علت می توان نوشت:

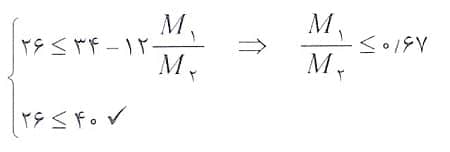
بنابراین گزینه 2 صحیح است.

مثال: یک عضو بتنی فشاری مهار شده (k=1) با ابعاد مقطع 400×400 mm تحت اثر لنگرهای خمشی M₁=M₂ مطابق شکل قرار دارد. برای آن که بتوان از اثر لاغری در این عضو صرف نظر کرد حداکثر طول آزاد آن باید به کدامیک از اعداد زیر نزدیکتر باشد؟ (شعاع ژیراسیون برابر 0.3 بعد مقطع در نظر گرفته شود)

1)6 متر                   2)2.65 متر                   3)4.8 متر              4)5.5 متر

حل: عضو مهار شده است و داریم:

با توجه به اینکه مطابق شکل سوال در ستون انحنای مضاعف ایجاد می شود بنابراین نسبت M₁/M₂ مثبت می باشد.

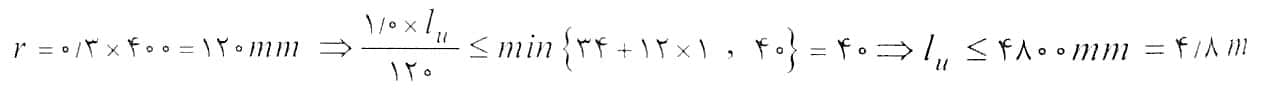
بنابراین گزینه 3 صحیح است.

مثال: در یک قاب خمشی، چنانچه ابعاد ستون ها 50×50 cm و ابعاد تیرها 40×60 cm و فاصله محور تا محور تیرهای طبقات 300 سانتی متر و ضریب طول موثر ستون k=1.2 متر باشد، در مورد طراحی آرماتورهای ستون گزینه صحیح را انتخاب کنید؟

1-صرف نظر کردن از اثر لاغری در این ستون بستگی به لنگرهای خمشی دو انتهای ستون دارد.

2-صرف نظر کردن از اثر لاغری در این ستون بستگی به مقدار آرماتورهای طولی ستون دارد.

3-می توان از اثر لاغری ستون صرف نظر کرد.

4-نمی توان از اثر لاغری ستون صرف نظر کرد.

حل: به نظر شما این ستون مهار شده است یا مهار نشده است؟ برای تشخیص وضعیت مهار شدگی ستون به دو نکته زیر دقت کنید:

1)سازه های با سیستم قاب خمشی معمولا مهار نشده محسوب می شوند، هر چند که برای بررسی دقیق تر آنها باید شاخص پایداری طبقات محاسبه گردد.

2)در سازه های مهار شده، ضریب طول موثر حداکثر برابر یک و در سازه های مهار نشده ضریب طول موثر بزرگتر از یک می باشد. بنابراین مشخص است که در این سوال ستون وضعیت مهار نشده دارد.

همانطور که خواندید در ستون های مهار نشده چنانه kl_u/r≤22 باشد، می توان از اثر لاغری در طراحی صرف نظر نمود.

با توجه به اطلاعات داده شده در این سوال و محاسبه طول آزاد ستون با توجه به ارتفاع تیرها داریم:

بنابراین می توان از اثر لاغری صرف نظر کرد و گزینه 3 صحیح است.

مطلب بعدی: تشدید لنگر خمشی

پیج اینستاگرام سیویل 2