ظرفیت خمشی مقاطع T شکل

ظرفیت خمشی مقاطع T شکل

در سه قسمت قبل با هندسه مقاطع بالدار و ضوابط آیین نامه ای آنها آشنا شدیم.

به منظور تکمیل بحث طراحی تیرهای بتن آرمه با مقاطع بالدار، در این قسمت می خواهیم نحوه محاسبه ظرفیت خمشی اسمی این مقاطع را در حالت شکست نرم (A_s<A_sb^T) بررسی کنیم.

در این خصوص باید توجه نمود که فرضیات و روش محاسبه مقاطع تک آرمه بوده و تنها عامل تفاوت، وجود بال های فشاری در این مقاطع می باشد.

مفهوم عملکرد مقطع T شکل

همانطور که قبلا در مورد مقاطع مستطیلی مطالعه کردیم، بلوک تنش فشاری و معادلات حاکم بر مقطع تنها در یک حالت محاسبه شد، که دلیل این امر ثابت بودن عرض مقطع مستطیلی در تمام ارتفاع آن می باشد.

اما در مقاطع T شکل عرض مقطع در تمام ارتفاع آن ثابت نبوده، به همین دلیل با توجه به موقعیت قرار گیری محور خنثی و ارتفاع بلوک فشاری یکنواخت (a)، در لحظه نهایی یکی از دو حالت زیر رخ می دهد:

1- بلوک تنش فشاری معادل، در بال تیر قرار گیرد (a≤h_f):

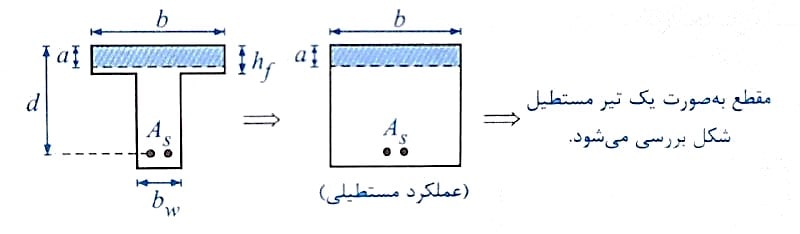
در این حالت می توان در ذهن اینگونه فرض نمود که قسمت های خالی مقطع نیز دارای بتن بوده و به عبارتی برخلاف ظاهر، از نظر عملکرد خمشی، تیر T شکل مانند یک مقطع مستطیلی ساده عمل می کند.

در این حالت محاسبات مقطع مانند یک مقطع مستطیلی با عرض b و ارتفاع موثر d مطابق آنچه در فصل قبل گفتیم انجام می شود.

2- بلوک تنش فشاری معادل، در بال و جان قرار گیرد (a>h_f):

در این حالت عملکرد مقطع تیر به صورت T شکل در نظر گرفته می شود. در واقع مطابق شکل بالا، سطح هاشور خورده تحت تنش فشاری قرار گرفته و از این رو محاسبات مربوط به نیرو و همچنین لنگر خمشی در این حالت با توجه به مساحت تحت فشار و هندسه T شکل در نظر گرفته می شود.

با توجه به تقسیم بندی فوق واضح است که در حالت اول، برای تحلیل از روابط فصل دوم و در حالت دوم باید از روابط خاص مقطع T شکل مطابق ضوابط این قسمت استفاده کنیم.  در این حالت برای محاسبه مقاومت خمشی مقطع و سایر پارامترهای آن، از ایده جداسازی مقطع استفاده می کنیم.

تذکر: برای تشخیص عملکرد مقطع در لحظه نهایی، ابتدا فرض می کنیم که عملکرد مقطع به صورت مستطیلی است و پارامتر زیر را محاسبه می کنیم:

در ادامه متناسب با مقدار a دو حالت زیر رخ می دهد:

روش جداسازی مقاطع T شکل

مشابه با توضیحات مطرح شده در قسمت قبل، روش جداسازی مقاطع یک ایده ساده و جایگزین برای حل معادلات مقاطع بالدار ارائه می دهد، به نحوی که با استفاده از این روش، پارامترهای اساسی مقطع به راحتی و طی دو مرحله قابل محاسبه می باشد.

در این روش با مجزا نمودن بال و جان مقطع ازیکدیگر، تحلیل مقطع بر اساس شکل های (B) و (C) مطابق آنچه نشان داده شده است انجام می گردد:

با توجه به شکل های فوق، تحلیل مقطع و محاسبه ظرفیت خمشی آن مطابق گام های زیر انجام می شود:

گام اول: مطابق شکل شماره (C) بخشی از فولاد کششی کل، صرف به تعادل رساندن نیروی فشاری بال ها می شود. در این صورت سهم فولاد کششی بال ها مطابق رابطه تعادل به صورت زیر بدست می آید:

A_sf: سهم فولاد کششی برای برقراری تعادل با نیروی فشاری بال ها.

گام دوم: با مشخص شدن مقدار فولاد سهم بال، مساحت فولاد مصرفی برای به تعادل رساندن مقطع شکل (B) با توجه به کل فولاد کششی مقطع به صورت زیر بدست می آید:

A_sw: سهم فولاد کششی برای برقراری تعادل با نیروی فشاری جان.

A_s: کل فولاد کششی مقطع.

در این صورت عمق بلوک فشاری مقطع (B) با استفاده از رابطه تعادل به صورت زیر بدست می آید:

گام سوم: با توجه به مشخص بودن پارامترهای مقاطع (B) و (C)، سهم لنگر خمشی اسمی هر یک از این مقاطع به صورت زیر محاسبه می شود:

M_nf: لنگر خمشی اسمی ناشی از بال های فشاری مقطع.

M_nw: لنگر خمشی اسمی ناشی از جان مقطع

گام چهارم: با توجه به گام قبل، کل لنگر خمشی اسمی مقطع برابر مجموع لنگرهای خمشی اسمی بال و جان بوده و به صورت زیر محاسبه می شود:

M_n: لنگر خمشی اسمی مقطع بالدار.

بررسی یک سوال

حداکثر مقدار لنگری که می توان به مقاطع T شکل اعمال نمود چقدر می باشد؟

پاسخ:

همانطورکه در فصل دوم خواندیم، حداکثر مقدار لنگر قابل تحمل تیرها از حاصلضرب ضریب کاهشی φ در مقدار لنگر خمشی اسمی بدست می آید. در تیرهای T شکل نیز مشابه تیرهای مستطیلی، ضریب φ براساس وضعیت مقطع در لحظه نهایی بدست می آید.

M_u<φM_n

توجه شود با توجه به اینکه طراحی اعضای خمشی با نیروی محوری فشاری نهایی کمتر از 0.1f^’_cA_g باید به صورت کشش – کنترل باشد، در آیین نامه (A_s≤A_smax) ضریب φ=0.9 در نظر گرفته می شود.

مثال: در شکل زیر یک مقطع تیر بالدار نمایش داده شده است. در صورتی که آرماتورهای کششی به کار رفته در این مقطع 6φ28 باشد، ظرفیت خمشی اسمی این مقطع برابر کدامیک از گزینه های زیر می باشد؟ (بتن مصرفی از رده C30 و فولاد S400 می باشد. ابعاد داده شده بر روی شکل بر حسب میلی متر می باشد.)

1- 541                    2- 710                3- 684                        4- 638

حل:

ابتدا برای تعیین عملکرد مقطع، عمق بلوک فشاری را در لحظه نهایی با فرض اینکه بلوک فشاری در بال واقع شده است و با فرض b=600 mm محاسبه می کنیم:

بنابراین فرض انجام شده صحیح نمی باشد و مقطع عملکرد T شکل دارد.

a=96.6 mm > h_f=80 mm

مطابق گام بندی عنوان شده، با توجه به ایده جداسازی، ابتدا سهم فولاد کششی بال ها را محاسبه می کنیم:

نکته: هنگامی که آرماتورهای کششی در دو یا چند ردیف به کار رفته باشند، عمق محور خنثی در محاسبات لنگر خمشی، برابر فاصله مرکز سطح آرماتورهای کششی تا دورترین تار فشاری بتن در نظر گرفته می شود. در این صورت برای تعیین مرکز ثقل آرماتورها می توان از رابطه زیر استفاده کرد:

A_i: مساحت مقطع میلگرد i ام.

Y_i: فاصله مرکز سطح میلگرد i ام تا مبدا مورد نظر.

در این سوال با توجه به یکسان بودن تعداد و قطر آرماتورها در هر دو ردیف، مشخص است که مرکز سطح آرماتورها در وسط فاصله آنها، یعنی در فاصله 60+60/2=90 mm از تار پایین مقطع قرار گرفته است.

بنابراین گزینه 2 صحیح است.

مثال: یک تیر بتن آرمه با مقطعی مطابق شکل زیر، تحت لنگر نهایی ضریبدار مثبت قرار دارد. چنانچه در حالت نهایی کرنش فولادهای مقطع برابر 0.014 باشد، لنگر خمشی مقاوم مقطع در این حالت چند کیلونیوتن است؟ بتن C30 و فولاد S400 و عمق موثر مقطع برابر 420 میلی متر در نظر گرفته می شود. ابعاد مشخص شده به میلی متر هستند.

1)470                    2)370                               3)330                          4)430

حل: برای محاسبه لنگر خمشی مقاوم مقطع، با توجه به اینکه مقدار کرنش نهایی فولادها داده شده، با استفاده از نمودار کرنش ها مقدار عمق محور خنثی و سپس عمق بلوک فشاری یکنواخت را محاسبه می کنیم:

در ادامه با توجه به اینکه در لحظه نهایی Ԑ_s=0.014≥Ԑ_y+0.003=0.005 می باشد، عملکرد مقطع به صورت کشش – کنترل بوده و ضریب φ=0.9 در نظر گرفته می شود.

تذکر: باید دقت شود که آرماتور به کار رفته در این مقطع از مقدار حداقل بیشتر است.

مثال: تحت لنگر خمشی مثبت، لنگر اسمی مقطع تیر I شکل نشان داده شده برابر M_n می باشد. در این صورت لنگر اسمی مقطع جعبه ای برابر است با:

حل:

در مقایسه با لنگر خمشی این دو مقطع ابتدا به موارد زیر توجه شود:

1)عرض و ضخامت بال فشاری برای هر دو مقطع یکسان است.

2)ارتفاع موثر و ضخامت جان برای هر دو مقطع یکسان است.

3)مقدار فولاد دو مقطع یکسان است.

با توجه به این موارد مقطع I و جعبه ای نشان داده شده تحت خمش هیچ تفاوتی با یکدیگر ندارند؛ پس محور خنثی در هر ارتفاعی قرار گیرد، رفتار این دو مقطع یکسان است.

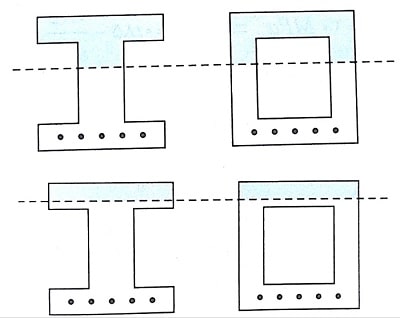
با توجه به شکل های فوق، در هر صورت مساحت ناحیه فشاری و بازوی لنگر برای هر دو مقطع یکسان است که باعث می شود لنگر یکسانی را ایجاد کنند و گزینه 1 درست می باشد.

مطلب بعدی: ضوابط تیرچه ها

پیج اینستاگرام سیویل 2