ضوابط طراحی دیوارهای باربر و غیر باربر بتنی
ضوابط طراحی دیوارهای باربر و غیر باربر بتنی
بخش اول: طراحی دیوار تحت بار محوری
مقدمه:
دیوارها از گذشته تاکنون به عنوان یکی از ارکان اصلی سازه ای در ساختمان ها مورد استفاده قرار گرفته اند. این اعضای صفحه ای قادر به تحمل انواع نیروهای محوری، برشی و لنگرهای خمشی بوده و معمولا براسا وجود یا عدم وجود بار محوری طبقه بندی می شوند. انواع دیوارهای بتن آرمه را می توان در دو گروه کلی در نظر گرفت:
1 – دیوارهای غیر باربر:
در صورتی که دیوار در سیستم باربری ثقلی سازه به طور مستقیم نقشی نداشته باشد، دیوار غیر باربر در نظر گرفته می شود.
البته باید توجه نمود که این دیوارها ممکن است تحت اثر بارهای برشی عمود بر صفحه قرار بگیرند. در واقع دیوارهای حائل و یا دیوارهای زیر زمین که به شکل مجزا از سازه اجرا شده اند در این گروه قرار دارند.
2- دیوارهای باربر:
دیوارهایی هستند که مستقیما در سیستم باربری سازه نقش اساسی دارند. در این حالت معمولا سیستم باربر می تواند شامل سیستم باربر قائم و همچنین جانبی بوده و بارهای طراحی دیوار براساس عملکرد آن مشخص می گردد.
به طور مثال دیوارهایی که تحمل و انتقال بارهای ثقلی نقش دارند، عمدتا تحت نیروهای محوری بزرگ و لنگرهای خمشی نسبتا کوچک قرار می گیرند. این گونه دیوارها معمولا در سیستم های دال و دیوار وجود دارند.
دقت شود در این حالت تعداد دیوارهایی که به عنوان المان قائم به کار رفته اند، قابل توجه است. از طرفی در سیستم هایی که از دیوار به عنوان عمل باربر جانبی استفاده می شود و در واقع سیستم باربر ساختمان از نوع دوگانه (قاب و دیوار) در نظر گرفته شده است، دیوارها عمدتا به منظور تحمل نیروی برشی ناشی از بارهای جانبی از قبیل باد و زلزله به کار می روند.
با توجه به نیروهای وارد بر دیوار، این نوع دیوارها به دیوارهای برشی معروف هستند. در ادامه به شرح شرایط و بیان ضوابط آیین نامه ای در خصوص طراحی دیوار تحت اثر بارهای وارد بر آن می پردازیم.
محاسبه مقاومت مورد نیاز دیوار
همانطور که گفته شد، دیوارها تحت نیروهای مختلفی قرار می گیرند. بر این اساس لازم است مقاومت دیوار تحت اثر هر یک از عوامل کنترل شده و با رعایت اثرات اندرکنشی بارها از تامین مقاومت کافی دیوار اطمینان حاصل نمود.
با توجه به نیروهای اصلی وارد بر دیوار، مقاومت آن براساس روابط زیر کنترل می شود:

در روابط فوق Vu ، Mu ، Pu به ترتیب نیروی محوری، لنگر خمشی و نیروی برشی نهایی ضریبدار وارد بر دیوار بوده و Vn ، Mn ، Pn به ترتیب مقاومت فشاری محوری اسمی ، مقاومت خمشی اسمی و مقاومت برشی اسمی دیوار هستند.
تذکر 1 : دقت کنید با توجه به اینکه دیوارا عملکردی مشابه ستون ها ها دارند، لذا معمولا در لحظه نهایی به صورت فشار – کنترل در نظر گرفته می شوند و به همین دلیل از ضریب کاهنده فی 0.65 در خصوص کنترل مقاومت محوری آنها استفاده شده است.
هر چند در صورتی که با توجه به وضعیت نهایی دیوار مشخص شود که دیوار وضعیت مششی – کنترل و یا حالت انتقالی را دارد، می توان از ضرایب مربوطه مطابق فصل ستون ها نیز استفاده کرد.
تذکر 2 : در دیوارهای غیر باربر، با توجه به عدم حضور بار محوری قابل توجه، مقاومت خمشی اسمی آنها تابعی از نیروی محوری نخواهد بود و محاسبات آنها مانند تیرها انجام می شود.
مقاومت فشاری محوری اسمی دیوار
همانطور که در تذکر فوق خواندیم، عملکرد دیوارهای باربر، خصوصا دیوارهایی که تحت اثر نیروهای محوری قابل توجه قرار دارند، مشابه ستون ها بوده لذا در اغلب موارد ضوابط طراحی آنها مشابه ستون ها در نظر گرفته می شود.
همانطور که در فصل ستون ها خواندیم، در صورتی که ستون فقط تحت نیروی محوری خالص قرار گرفته باشد، مقدار حداکثر مقاومت فشاری اسمی ستون برابر Pn,max در نظر گرفته می شود. در دیوارها نیز به همین صورت در نظر گرفته می شود با این تفاوت که در دیوار حتی در صورت اعمال لنگر خمشی به همراه نیروی محوری فشاری نیز مقدار حداکثر نیروی محوری فشاری قابل اعمال به دیوار به صورت زیر بدست می آید:
Pu≤ΦPn,max
روش تجربی: به طور کلی طراحی دیوارها تحت اثر همزمان نیروی محوری و لنگر خمشی داخل یا خارج از صفحه مطابق ستون ها انجام می شود، اما در دیوارهایی با مقطع مستطیل توپر که تحت اثر نیروی محوری و لنگر خمشی خارج از صفحه به نحوی قرار گرفته اند که در آنها خروج از مرکزیت برآیند بارهای ضریبدار کمتر از یک ششم ضخامت دیوار می باشد e≤h/6، برای محاسبه مقاومت اسمی محوری مقطع می توان از رابطه تجربی زیر استفاده کرد:


Pn: مقاومت فشاری محوری اسمی، نیوتن.
Ag: مساحت مقطع افقی دیوار، میلی متر مربع.
k: ضریب طول موثر دیوار در جهت خارج از صفحه.
lc: فاصله بین مرکز تا مرکز گره های انتهایی دیوار در جهت ارتفاعی، میلی متر.
h: ضخامت دیوار، میلی متر.
در رابطه بالا برای محاسبه مقدار ضریب طول موثر دیوار، با توجه به شرایط تکیه گاهی از موارد زیر استفاده می شود:
1- در دیوارهای نهار شده در مقابل حرکت جانبی در بالا و پایین که در آنها از چرخش در یک یا هر دو انتها (بالا و پایین دیوار) جلوگیری به عمل آمده باشد، ضریب k برابر 0.8 می باشد.
2- در دیوارهای مهار شده در برابر حرکت جانبی در بالا و پایین که در آنها از چرخش در دو انتها جلوگیری به عمل نیامده باشد، یعنی امکان چرخش هر دو انتها وجود داشته باشد، ضریب k برابر 1 فرض می شود.
3- در دیوارهای مهار نشده در برابر حرکت جانبی ضریب k برای 2 در نظر گرفته می شود.
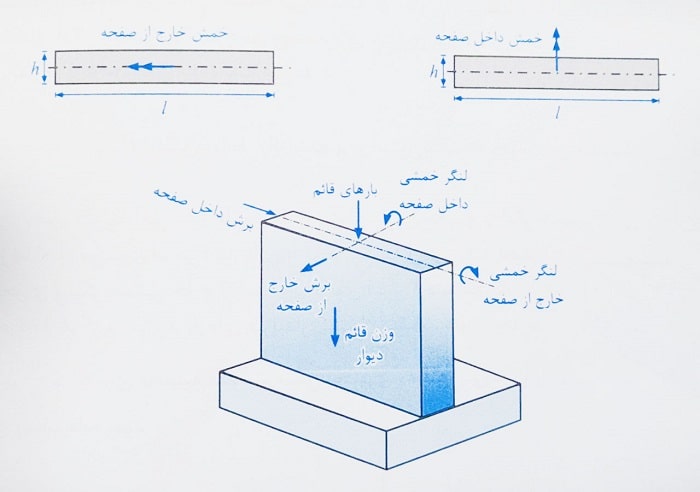
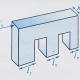
یادآوری: محور خمش خارج از صفحه در راستای محور طولی دیوار و محور خمش داخل صفحه عمود بر محور طولی دیوار می باشد، برای درک بهتر به شکل های زیر که یک دیوار را تحت بارهای مختلف به همراه پلان آن و محورهای خمش مذکور نمایش می دهد توجه کنید:
l: طول افقی دیوار.
حداقل ضخامت دیوار
مانند سایر اعضای بتن آرمه، دیوارها نیز باید به لحاظ هندسه باید ضوابط خاصی را رعایت کنند. با توجه به عملکرد صفحه ای دیوارها، ضابطه آیین نامه ای دیوار توسط ضخامت آن و براساس موارد زیر کنترل می شود.
در این خصوص استفاده از ضخامت های کمتر تنها در شرایطی که مقاومت و پایداری دیوار تحت اثر بارهای اعمالی توسط تحلیل سازه کنترل شده باشد، مجاز است.
1- دیوارهای باربر و دیوارهای سازه ای با شکل پذیری کم:
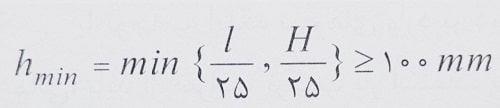
l: طول مهار نشده دیوار
H: ارتفاع مهار نشده دیوار
2- دیوارهای بیرونی زیر زمین ها و دیوارهای شالوده و سایر دیوارهایی که در تماس دائم با خاک قرار دارند:
h: 200 mm
مقدار حداقل ضخامت صرفا برای دیوارهایی کاربرد دارد که مطابق روش تجربی بالا طراحی شده باشند.
3- در دیوارهای غیر باربر، حداقل ضخامت به صورت زیر محاسبه می گردد:
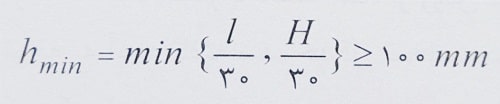
مثال: یک دیوار باربر بتن آرمه با ضخامت 250 میلی متر و ارتفاع 4 متر را در نظر بگیرید. در صورتی که بتن مصرفی از رده C30 باشد، مقدار مقاومت فشاری محوری اسمی این دیوار در هر متر از طول آن بدون لحاظ کردن خروج از محوریت بار محوری به روش تجربی، چند کیلو نیوتن می باشد؟ دیوار به صورت مهار شده بوده و چرخش در دو انتها آزاد می باشد.
1- 2875 2- 3094 3- 3653 4- 2463
حل: با توجه به اینکه از خروج از مرکزیت بارمحوری صرف نظر شده است، بنابراین داریم:
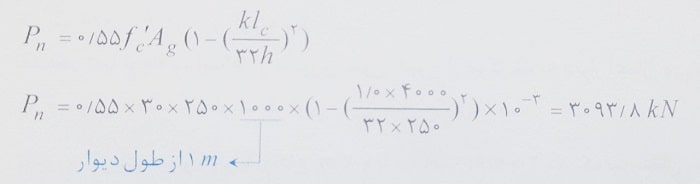
بنابراین گزینه 2 صحیح است.
مثال: در یک دیوار باربر بتن آرمه به ارتفاع 3 متر که متعلق به یک ساختمان 3 طبقه است، نیروهای محوری ناشی از بارهای مرده و زنده وارده به ترتیب برابر 3500 و 1800 کیلونیوتن بدست آمده است. در این دیوار مهار شده در برابر حرکت جانبی که 5 متر طول دارد، دیتایل اجرای دیوار به کف به نحوی است که چرخش تنها در یک انتهای دیوار مقید می باشد. در صورتی که نیروهای وارده به صورت محوری و بدون خروج از مرکزیت در نظر گرفته شوند، حداقل ضخامت دیوار به روش تجربی چقدر باشد تا مقاومت آن در برابر بارهای وارده کافی باشد؟ f’c = 25
1- 300 2- 150 3- 250 4- 200 میلی متر
حل: با توجه به اینکه نیروهای وارد بر دیوار به صورت مجزا داده شده اند، بنابراین برای محاسبه بار نهایی اعمالی، باید از ضرایب ترکیب بار استفاده کنیم. بنابراین:
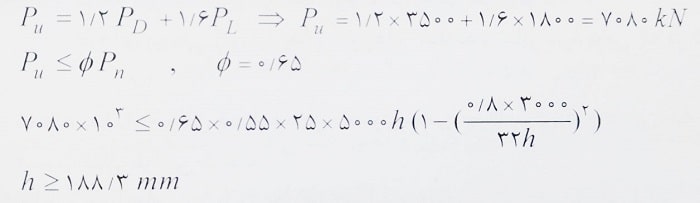
حالا باید مقدار بدست آمده را با حداقل مجاز مقایسه کنیم:
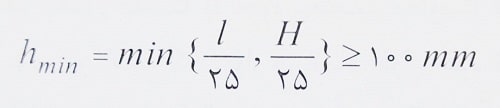
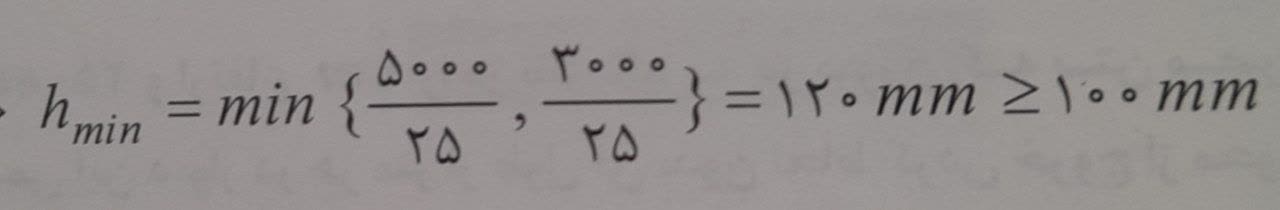
بنابراین ضخامت از مقدار مجاز حداقل بیشتر بوده و گزینه 4 ضخامت 200 میلی متر صحیح می باشد.
مثال: یک دیوار باربر با ارتفاع 7 متر و با ضخامت 200 میلی متر در یک ساختمان به کار رفته است. با توجه به کنترل ضوابط آیین نامه در خصوص هندسه دیوار، به سوالات زیر پاسخ دهید (دیوار در تماس با خاک نمی باشد).
الف – حداکثر طول این دیوار در طراحی به روش تجربی چقدر است؟
ب – چنانچه دیوار غیر باربر باشد، مقدار حداکثر طول مجاز آن چگونه تغییر می کند؟
حل: الف) می دانیم در دیوارهای باربر طراحی شده با روش تجربی، مقدار حداقل ضخامت به صورت زیر بدست می آید:
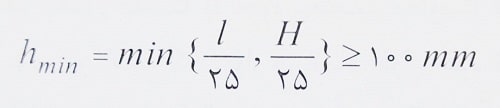
با توجه به ارتفاع 7 متری دیوار، مقدار نسبت H/25 برابر 280 بدست می آید که با توجه به اینکه ضخامت حداقل دیوار 200 میلی متر است، مشخص است که مقدار l/25 در تعیین حداقل ضخامت دیوار کنترل کننده بوده است، بنابراین داریم:

یعنی با توجه به ضخامت 200 میلی متری دیوار، حداکثر طول باید 5 متر باشد تا ضوابط هندسی دیوار رعایت شود.
ب) در دیوارهای غیر باربر داریم:
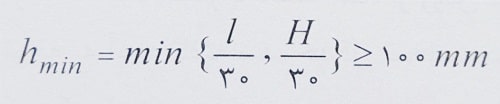
با توجه به روش حل قسمت الف، به دلیل اینکه h=200 < H/30 = 7000/30 = 233 mm است، داریم:
h= 200 mm ≥ l/30 ⇒ l≤6000 mm
یعنی چنانچه دیوار غیر باربر باشد می تواند طولی حداکثر 6 متر داشته باشد.
مثال: یک دیوار باربر بتن آرمه درجا دارای ضخامت 200 میلی متر و طول 4 متر بوده و فاصله قائم آزاد بین تکیه گاه بالا و پایین دیوار برابر 3.6 متر است. از چرخش دیوار در بالا و پایین آن جلوگیری شده است و دیوار در مقابل هر حرکت جانبی مهار شده است. مقاومت اسمی مقطع در برابر بار محوری با استفاده از رابطه تجربی و با فرض اینکه دیوار فقط تحت اثر بار محوری فشاری باشد، بر حسب KN به کدامیک از مقادیر زیر نزدیکتر است؟ مقاومت فشاری مشخصه بتن 25 مگاپاسکال است.
1- 6032 2- 7520 3- 5702 4- 8772
حل: با توجه به اینکه دیوار فقط تحت اثر نیروی محوری فشاری است بنابراین خروج از مرکزیت آن صفر است و مقدار مقاومت فشاری محوری اسمی آن از رابطه زیر قابل محاسبه است:
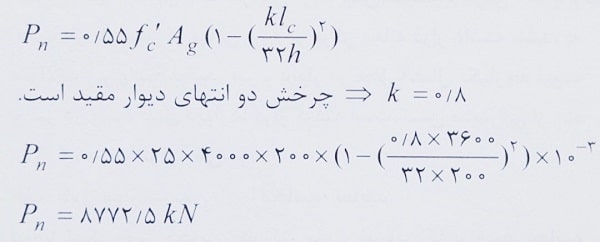
بنابراین گزینه 4 صحیح است.
طول موثر دیوار تحت اثر بار متمرکز
در بخش گذشته با نحوه محاسبه مقاومت فشاری دیوارها آشنا شدیم. آنچه در محاسبات گذشته حائز اهمیت بود، این است که دیوار در تمام طول خود تحت اثر بارگذاری قائم قرار گرفته است، به عبارتی دیوار تحت بارهای گسترده مشابه حالتی که به عنوان تکیه گاه سراسری کف سازه ای به کار می رود، در نظر گرفته شده است.
به همین دلیل در محاسبات مربوط به مقاومت فشاری نیز کل طول دیوار به عنوان طول موثر در برابر نیرو در محاسبه پارامتر Ag لحاظ شد. اما در صورتی که بار قائم وارد بر دیوار به صورت متمرکز بر آن اعمال شود، به دلیل تمرکز بار تنها در قسمت مشخصی از دیوار، نمی توان پارامتر Ag را برابر مساحت کل مقطع در نظر گرفت. در چنین مواردی طول موثر دیوار نباید از موارد زیر بیشتر در نظر گرفته شود:
1- عرض سطح اعمال بار به اضافه دو برابر ضخامت دیوار در هر طرف سطح اثر بار.
2- فاصله مرکز تا مرکز بارهای متمرکز.
در این حالت با محاسبه طول موثر دیوار و ضرب آن در مقدار ضخامت دیوار، پارامتر Ag محاسبه می شود.
لازم به ذکر است طول افقی موثر بار نباید خارج از درزهای قائم دیوار قرار بگیرد، مگر اینکه روش انتقال نیروها در محل درزها به طور مناسب انجام و در طراحی لحاظ شده باشد.
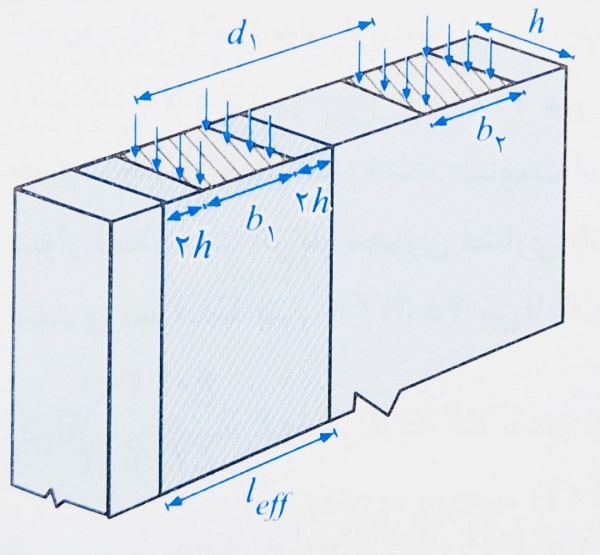
برای درک بهتر این موضوع به شکل زیر که یک دیوار را با دو بار متمرکز نشان می دهد توجه کنید. دقت شود بار متمرکز در واقعیت به صورت نقطه ای اعمال نشده، بلکه از طریق سطحی نسبتا کوچک مشابه آنچه در شکل نشان داده شده بر دیوار اعمال می شود ( عرض اعمال بار نسبت به کل طول دیوار ناچیز است).
b1 و b2: طول سطح اثر بارهای متمرکز (متمرکز معادل)
d1: فاصله سطح اثر بارهای متمرکز – فاصله مرکز تا مرکز b1 و b2 می باشد.
leff: طول افقی دیوار.

مثال: دو دیوار بتن آرمه به ضخامت 200 میلی متر و طول 4 متر که در فاصله 6 متری از یکدیگر قرار گرفته اند، به عنوان تکیه گاه های یک تیر بتن آرمه پیش ساخته با عرض 500 و ارتفاع 600 میلی متر به کار رفته اند. در صورتی که تیر تحت اثر بار متمرکز نهایی Qu در مرکز دهانه داشته باشد، به سوالات زیر پاسخ دهید. تیر و دیوار در محل اتصال یکپارچه نبوده و تیر در وسط طول دیوارها قرار گرفته است. بتن مصرفی از رده C25 می باشد.
الف) طول موثر نشیمن بار را محاسبه کنید.
ب) با کمک روش تجربی، حداکثر مقدار نیرویی که بر وسط دهانه تیر می توان اعمال کرد Qu با در نظر گرفتن مقاومت فشاری دیوار چقدر است؟
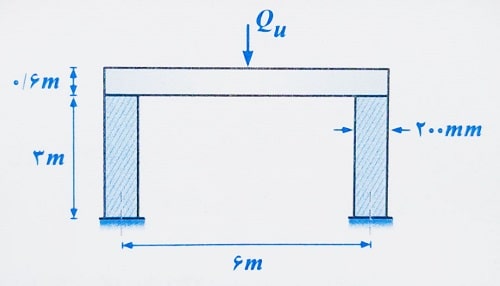
حل: الف) با توجه به اینکه بار از طریق تیر به دو دیوار اعمال می گردد، لذا ماهیت بار به صورت متمرکز بوده بنابراین مقدار طول موثر بار با توجه به اینکه عرض سطح اثر بار برابر عرض تیر می باشد، مطابق آنچه خواندیم برابر است با:
leff = b+4h = 500 +4×200 = 1300 mm
دقت شود با توجه به اینکه بار صرفا از یک تیر بر روی دو دیوار اعمال می شود، بنابراین فقط یک بار متمرکز بر روی هر دیوار وجود داشته و در نتیجه مورد دوم یعنی فاصله بارهای متمرکز در محاسبه طول موثر دیوار در نظر گرفته نشده است.
ب) با محاسبه طول موثر اعمال بار، پارامتر Ag به صورت زیر محاسبه می شود:
Ag = h x leff = 200 x 1300 = 26 x 10000 mm2
با توجه به اینکه تیر و دیوار در محل اتصال یکپارچه نیستند، لذا دیوار در قسمت فوقانی مهار نشده بوده، بنابراین ضریب طول موثر دیوار برابر 2 در نظر گرفته می شود.

چون تیر در هر دو طرف دارای تکیه گاه است بنابراین هر دیوار Qu/2 را تحمل می کند لذا کل نیروی قابل اعمال به تیر 2×281.4 = 562.8 KN می تواند باشد.
ضوابط طراحی دیوارهای باربر و غیر باربر بتنی – ضوابط طراحی دیوارهای باربر و غیر باربر بتنی – ضوابط طراحی دیوارهای باربر و غیر باربر بتنی – ضوابط طراحی دیوارهای باربر و غیر باربر بتنی



دیدگاه خود را ثبت کنید
تمایل دارید در گفتگوها شرکت کنید؟در گفتگو ها شرکت کنید.