ستون تحت بار محوری خالص
ستون تحت بار محوری خالص
اولین نکته ای که در خصوص ستون ها در ذهن ایجاد می شود، توانایی آنها در تحمل بارهای قائم طبقات و انتقال بارها به فونداسیون می باشد. این تعریف هر چند ساده به نظر می رسد اما ماهیت رفتاری ستون ها را به خوبی نشان می دهد.
در واقع یکی از مهمترین بارهایی که ستون ها تحمل می کنند، بارهای قائم مرده و زنده ناشی از طبقات است و به دلیل اینکه این بارهای قائم باعث ایجاد نیروهای فشاری در ستون می گردند، عمدتا به ستون ها اعضای فشاری نیز گفته می شود.
از طرفی می دانیم سازه ها علاوه بر بارهای قائم تحت بارهای جانبی نیز قرار می گیرند که این نیروهای جانبی باعث ایجاد نیروی محوری و لنگر خمشی در ستون ها می شود.
تحت اثر ترکیب نیروی محوری و لنگر خمشی در برخی از ستون ها، نیروهای کششی نیز ممکن است ایجاد شود که در این حالت مطابق آنچه در فصل خمش آموختید، آرماتورگذاری نقش مهمی در تحمل نیروهای کششی وارده خواهد داشت. در سازه های بتنی ستون ها به دو گروه کلی طبقه بندی می شوند:
ستون های کوتاه:
معمولا ستون های به کار رفته در ساختمان های متداول در این گروه قرار می گیرند. در این ستون ها مقاومت مقطع براساس هندسه و آرماتورگذاری آن بدست می آید.
ستون های لاغر:
در این حالت هندسه مقطع و ارتفاع ستون به نحوی است که اثر تغییرمکان های جانبی بر رفتار ستون و تعیین مقاومت آن قابل ملاحظه است. هر چند ستون های کوتاه و لاغر در بسیاری از مفاهیم اولیه طراحی نقاط مشترک زیادی دارند.
اما درخصوص تعیین مقاومت و پاسخ آنها تحت بارگذاری اعمالی، تفاوت هایی بین آنها وجود دارد. با توجه به این موضوع، مفهوم اولیه ستون ها یعنی ستون های کوتاه را با بررسی ضوابط آیین نامه ای و نحوه طراحی و محاسبه مقاومت مقطع در این فصل با شما عزیزان بررسی می نماییم و سپس در فصل هفتم به بررسی ستون های لاغر می پردازیم.
ستون تحت بار محوری خالص فشاری
به طور کلی منظور از بار محوری خالص فشاری، اعمال نیروی محوری فشاری بر مقطع ستون، بدون حضور هرگونه لنگر خمشی در آن می باشد. برای تحلیل این موضوع در حالت نهایی، به موارد زیر توجه کنید:
1- با توجه به اینکه نیروی محوری فشاری باعث ایجاد کرنش فشاری می شود، هنگامی که مقطع ستون تحت اثر نیروی محوری فشاری خالص قرار می گیرد، در تمام نقاط مقطع کرنش فشاری رخ داده و مقدار این کرنش نیز در تمام این نقاط ثابت خواهد بود.
برای درک بهتر این موضوع به مقطع ستون نشان داده شده در شکل زیر نگاه کنید که تحت اثر نیروی محوری فشاری خالص P قرار گرفته است. با توجه به توضیحات و شکل رسم شده، مقدار کرنش در تمام نقاط مقطع و همچنین آرماتورهای موجود در مقطع با هم برابرند. در این صورت می توان نوشت:
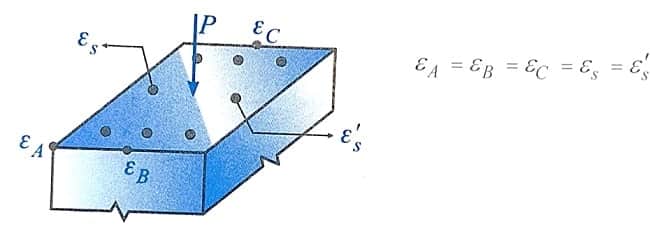
2- در ستون های تحت بار محوری خالص در لحظه نهایی، مقدار کرنش در تمام نقاط مقطع یکسان و برابر کرنش حد گسیختگی بتن (Ԑcu) می باشد.
![]()
3- با توجه به اینکه در فولادهای متدوال (از رده S240 تا S520) مقدار کرنش جاری شدن کمتر از کرنش گسیختگی بتن است، بنابراین در لحظه نهایی، تمام فولادهای مقطع در فشار جاری می شوند.
4- نمودار تنش و کرنش مقطع ستون در لحظه نهایی در یک مقطع مستطیلی با فرض وجود دو ردیف آرماتور که در دو وجه مقطع قرار گرفته اند، به صورت شکل زیر رسم می شود:
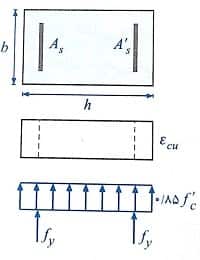
همانطور که مشاهده می کنید با توجه به یکسان بودن مقدار کرنش در تمام نقاط مقطع، نمودار کرنش به صورت مستطیلی یکنواخت در نظر گرفته شده و نمودار تنش ها هم به صورت مستطیلی و با شدت تنش یکنواخت برابر 0.85f’c در محاسبات لحاظ می گردد. باید دقت شود در این حالت عمق بلوک فشاری a برابر کل بعد مقطع است.
5- با توجه به توضیحات فوق، نیروی محوری فشاری خالص ستون به صورت زیر محاسبه می گردد:

Ac: مساحت بتن تحت تنش فشاری
As و A’s: فولادهای دو دوجه مقطع.
برای محاسبه مساحت بتن تحت تنش فشاری، کافی است مساحت کل مقطع محاسبه شده و مساحت فولادها از آن کسر گردد. در این صورت رابطه محاسبه نیروی محوری خالص به صورت زیر بازنویسی می شود:
![]()
P0: مقاومت محوری فشاری اسمی مقطع بدون وجود خروج از محوریت بار، نیوتن
Ag: مساحت کل مقطع بدون در نظر گرفتن آرماتورها، میلی متر مربع
Ast: مساحت کل آرماتورهای موجود در مقطع، میلی متر مربع
f’c: مقاومت فشاری مشخصه بتن، مگاپاسکال
Fy: مقاومت تسلیم آرماتورهای طولی مگاپاسکال
تذکر 1: همانطور که از فصل خمش به خاطر دارید، مقدار تنش فشاری برابر α1f’c در نظر گرفته میشد که در آن مقدار α1 برای f’c>55 Mpa بر حسب مقاومت فشاری f’c متغیر بوده، در حالی که مطابق رابطه گفته شده تنش فشاری برای انواع مختلف بتن با ضریب کاهشی ثابت 0.85 در نظر گرفته شده است.
در واقع کاربرد این ضریب مثل حالتی است که حداکثر مقاومت فشاری بتن برابر 55 مگاپاسکال لحاظ شده باشد. اما باید توجه نمود که در آیین نامه هیچ اشاره ای به این محدودیت مقاومت نشده است.
تذکر2: حداکثر تنش تسلیم آرماتورها در رابطه گفته شده به 550 مگاپاسکال محدود می شود. البته باید توجه نمود که مطابق این شرط تمام رده های میلگردهای آجدار تا S520 در ستون ها قابل استفاده هستند.
حداکثر مقاومت فشاری محوری اسمی ستون
با توجه به این که در واقعیت ممکن است در اثر توزیع غیر یکنواخت بارهای ثقلی و ناشاقولی در اجرای ستون و سایر موارد مشابه، نیروی اعمالی به صورت محوری خالص به ستون اعمال نشود و در اثر اعمال خروج از مرکزیت های اتفاقی مقداری لنگر خمشی نیز همراه با آن بر ستون اعمال گردد، بنابراین مطابق آیین نامه در طراحی، لحاظ نمودن نیروی محوری خالص به عنوان ظرفیت باربری ستون مجاز نبوده و به جای آن از حداکثر مقاومت فشاری محوری اسمی ستون (Pnmax) استفاده می شود.
مقدار این پارامتر با توجه به شکل مقطع و نوع آرماتورهای عرضی موجود در ستون، به صورت زیر محاسبه می گردد:

تذکر 1: در بسیاری از سوالات آزمون نظام مهندسی، هدف محاسبه حداکثر مقاومت فشاری اسمی ستون (Pnmax) بوده و نباید آن را با مقدار P0 اشتباه گرفت. در این گونه موارد در صورت سوال عباراتی نظیر حداکثر مقاومت فشاری اسمی، حداکثر ظرفیت باربری محوری اسمی و … مطرح می شود.
تذکر 2: در ستون های بتنی نسبت آرماتور موجود در مقطع بر حسب درصد، به صورت زیر محاسبه می شود:

بررسی یک موضوع
در قسمت های فوق با نحوه محاسبه مقاومت محوری مصالح و همچنین حداکثر مقاومت فشاری اسمی مقطع آشنا شدید. اما سوالی که ممکن است از خود پرسیده باشید این است که چه مقدار نیروی فشاری به صورت محوری می توان بر ستون بتن آرمه اعمال کرد بدون آنکه ستون دچار گسیختگی شود؟
برای پاسخ به این سوال همانطور که از مفاهیم فصل اول به خاطر دارید باید دقت نمایید که روش طراحی مقاطع بتن آرمه منطبق بر روش طرح مقاومت می باشد؛ یعن باید رابطه زیر برقرار باشد:
![]()
Pu: نیروی محوری نهایی ضریبدار
Φ: ضریب کاهش مقاومت
Pn: مقاومت فشاری محوری اسمی عضو
در ستون هایی که در لحظه نهایی رفتار آنها به صورت فشار – کنترل می باشد، ضریب کاهش مقاومت مطابق آنچه درفصل اول گفته شد، به صورت زیر تعیین می شود:

در واقع در این حالت با کاهش ظرفیت باربری مجاز ستون، از عملکرد مناسب ستون تحت اثر توام نیروی محوری و لنگرهای خمشی ناخواسته ای که در طراحی ستون در نظر گرفته نشده اند، اطمینان حاصل می شود.
در مقاطعی که در لحظه نهایی در ناحیه انتقال قرار دارند یعنی در لحظه نهایی کرنش خالص کششی در فولادهای کششی بیشتر از Ԑy و کمتر از Ԑy+0.003 است مقدار ضریب کاهش φ مطابق روابط زیر بدست می آید:

Ԑy: کرنش جاری شدن فولاد
Ԑt: کرنش خالص کششی در دورترین ردیف آرماتورها
دقت شود که در این حالت Ԑy را برای فولاد S420 می توان برابر 0.002 در نظر گرفت.
محاسبه حداکثر مقاومت کششی محوری اسمی ستون
ستون بتن آرمه ای را در نظر بگیرید که تحت اثر نیروی محوری کششی قرار گرفته است. به نظر شما این ستون بتنی چقدر می تواند نیروی کششی را تحمل کند؟ حتما مطالب فصل دوم را به خاطر دارید که بتن توانایی چندانی در تحمل کشش نداشته و به راحتی در اثر اعمال تنش های کششی دچار ترک خوردگی می شود.
برای محاسبه بیشترین نیروی کششی قابل تحمل در ستون ها نیز به طور مشابه فرض می شود که با زیاد شدن نیروی کششی، بتن ترک خورده و تنها فولادها می توانند نیروی کششی را تحمل نمایند.
با توجه به این موضوع مقدار حداکثر مقاومت کششی محوری اسمی ستون به صورت زیر بدست می آید:
Pnt,max=Astfy
Pnt,max: حداکثر مقاومت کششی محوری اسمی ستون، نیوتن.
Ast: مجموع مساحت فولادهای طولی واقع در مقطع، میلی متر مربع.
fy: مقاومت حد تسلیم آرماتورهای طولی، مگاپاسکال.
تذکر: با فرض اینکه کرنش فولادهای کششی در حالت نیروی کششی خالص از Ԑy+0.003 بیشتر است، ضریب φ را می توان مطابق حالت کشش – کنترل برابر 0.9 در نظر گرفت.
مثال: یک ستون بتن آرمه را مطابق شکل زیر در نظر بگیرید. در صورتی که ابعاد مقطع ستون 500 x 500 mm ، مصالح مصرفی بتن رده C30 و فولاد S400 و همچنین آرماتورهای به کار رفته شامل 12φ20 باشد، به موارد خواسته شده در سوالات زیر پاسخ دهید.
الف) مقاومت محوری اسمی بدون برون محوری عضو چند کیلونیوتن می باشد؟
ب) حداکثر مقاومت فشاری محوری اسمی عضو چند کیلونیوتن می باشد؟
ج) حداکثر مقاومت کششی محوری اسمی عضو چند برابر حداکثر مقاومت فشاری اسمی آن می باشد؟
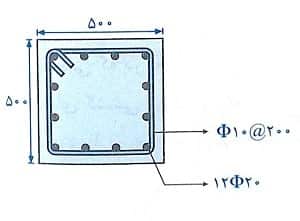
حل:
الف) مقدار P0 پرسیده شده و با توجه به رابطه فصل اول داریم:
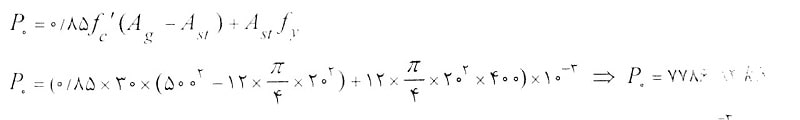
تذکر: ضریب-3 10 برای تبدیل واحد نیوتن به کیلو نیوتن استفاده شده است.
ب) با توجه به اینکه مقطع ستون مربعی بوده و در آن از تنگ های موازی استفاده شده است، حداکثر مقاومت فشاری اسمی محوری عضو برابر است با:
Pn,max = 0.8P0 = 0.8 x 7786.83 = 6229.47 kN
ج) مطابق فصل اول داریم:

مثال: در یک ستون بتن آرمه با مقطع دایره ای با آرماتورگذاری متقارن، حداکثر مقاومت فشاری محوری اسمی مقطع 4 برابر حداکثر مقاومت کششی اسمی عضو بدست آمده است. در صورتی که مصالح مصرفی C30 و S400 باشد، درصد تقریبی آرماتور به کار رفته در این ستون چقدر است؟ در ستون آرماتورهای عرضی به صورت دورپیچ به کار رفته اند.
1)1.4% 2)1.7% 3)1.9% 4)2.1%
حل: مطابق اطلاعات داده شده در سوال داریم:
Pn,max=4Pnt,max
با توجه به اینکه در این ستون از دورپیچ استفاده شده است داریم:
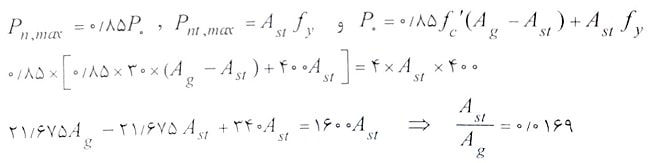
همانطور که گفته شد، در ستون ها نسبت آرماتور طولی برابر نسبت مساحت کل آرماتورها به مساحت کل مقطع می باشد و داریم:

بنابراین گزینه 2 صحیح است.
مثال: یک ستون بتن آرمه با ابعاد مقطع b x h که در آن از مصالح C25 و S400 استفاده شده است را در نظر بگیرید. آرماتورهای عرضی این ستون به قطر 10 mm بوده که با فواصل 150 mm در طول ستون به کار رفته اند. با توجه به مشخصات داده شده، در هر یک از موارد زیر حداکثر مقاومت فشاری محوری اسمی ستون چگونه تغییر می کند؟
الف) ابعاد مقطع ستون 20 درصد افزایش یابد ولی مساحت آرماتورهای ستون ثابت بماند.
ب) ابعاد مقطع ستون 20 درصد افزایش یابد ولی نسبت آرماتورهای ستون ثابت بماند.
ج) ابعاد مقطع ستون ثابت بماند ولی نسبت فولاد مصرفی ستون 20 درصد افزایش یابد.
حل:
الف) با افزایش ابعاد مقطع ستون و ثابت ماندن مساحت آرماتورهای آن خواهیم داشت:
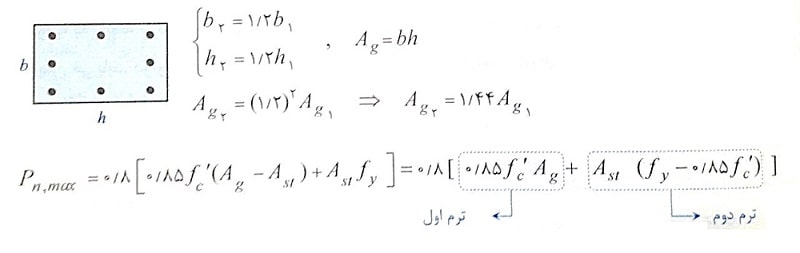
همانطور که در رابطه بالا مشاهده می شود، در شکل بازنویسی شده رابطه Pnmax به دلیل ثابت بودن مساحت آرماتورها، ترم دوم در هر دو حالت مقدار ثابتی دارد.
بنابراین اختلاف مقادیر مقاومت فشاری به ترم اول بستگی دارد؛ از طرفی با افزایش ابعاد مقطع به مقدار 20 درصد، مساحت مقطع به اندازه 44 درصد افزایش می یابد.
در این حالت به دلیل ثابت بودن پارامتر Ast ، ترم اول این رابطه 1.44 برابر شده و خواهیم داشت:

بنابراین با ثابت بودن ترم دوم، می توان گفت که در کل در این حالت حداکثر مقاومت فشاری محوری اسمی ستون کمتر از 44 درصد افزایش می یابد.
ب) با افزایش ابعاد مقطع و ثابت بودن درصد آرماتورهای ستون داریم:

با توجه به رابطه Pnmax مشاهده می شود که هر دو ترم رابطه بازنویسی شده 1.44 برابر شده اند. بنابراین در این حالت حداکثر مقاومت فشاری محوری اسمی ستون 44 درصد افزایش می یابد.
ج) در این حالت با ثابت بودن ابعاد مقطع و افزایش درصد فولاد مقطع، در واقع فقط مساحت فولادها افزایش یافته است بنابراین خواهیم داشت:
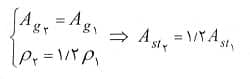
با توجه به رابطه بازنویسی شده Pnmax در این حالت ترم اول رابطه ثابت و از طرفی ترم دوم بیست درصد افزایش می یابد. در واقع می توان گفت در این حالت حداکثر مقاومت فشاری محوری اسمی ستون کمتر از 20 درصد افزایش خواهد یافت.

مثال: نسبت حداکثر مقامت فشاری محوری اسمی به حداکثر مقاومت کششی محوری اسمی یک ستون بتنی با مقطع شکل زیر با تنگ های موازی به کدامیک از مقادیر زیر نزدیک تر است؟ (رده بتن C25 و فولاد میلگرد S400 است).
1)2.9 2)2 3)3.1 4)2.5

حل: با توجه به اینکه در ستون از تنگ های موازی استفاده شده است داریم:

بنابراین گزینه 3 صحیح است.
مثال: در یک ساختمان بتن آرمه با سیستم قاب خمشی، مقدار مقاومت محوری اسمی فشاری یکی از ستون ها در حالت بدون خروج از مرکزیت، برابر 35Ag بر حسب نیوتن بدست آمده است. چنانچه حداکثر مقاومت کششی محوری اسمی این ستون برابر 1400 kN باشد، ابعاد در نظر گرفته شده برای طراحی این ستون به کدامیک از گزینه های زیر نزدیکتر می باشد؟ مصالح مصرفی C35 و S400 فرض می شود. Ag بر حسب میلی متر مربع در نظر گرفته می شود.
1- 450*450 2- 600*600 3- 500*500 4- 550*550
حل: با کمی دقت در سوال می توان متوجه شد که پارامترهای P0 و Pnt,max داده شده اند، بنابراین با توجه به روابطی که آموختیم خواهیم داشت:
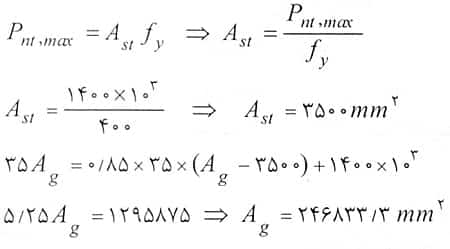
باتوجه به اینکه مقطع ستون در تمام گزینه های به صورت مربعی در نظر گرفته شده داریم:
b2=Ag b=496.8 mm
بنابراین با توجه به گزینه ها ابعاد مقطع ستون به 500 x 500 mm نزدیکتر بوده و گزینه 3 صحیح است.
مثال: در طراحی یک ستون بتنی با مقطع دایره ای برای یک ترکیب بارگذاری خاص، تمام ضوابط فنی رعایت و نسبت Su (نیروی ایجاد شده در مقطع یا نیروی نهایی موجود) به Sr (نیروی مقاوم مقطع)، با فرض استفاده از میلگردهای دورپیچ 0.97 محاسبه شده است.
اگر با رعایت تمام ضوابط فنی، در این ستون به جای میلگرد دورپیچ از تنگ های موازی معادل آن استفاده شود، در مورد نسبت Su به Sr کدام گزینه صحیح خواهد بود؟ (توجه شود که در ترکیب بارگذاری مورد نظر، برش نهایی در ستون در برابر نیروی مقاوم برشی مقطع ناچیز و غیر کنترل کننده می باشد)
1)نسبت Su به Sr حدود 15 درصد افزایش می یابد.
2) نسبت Su به Sr ممکن است حداکثر به 1.19 برسد.
3) نسبت Su به Sr تغییر نمی کند.
4) نسبت Su به Sr کاهش می یابد.
حل: همانطور که گفتیم، در طراحی ستون ها باید رابطه زیر برقرار باشد:
![]()
Pu: نیروی محوری ضریبدار نهایی وارد بر مقطع
Pn: مقاومت فشاری محوری اسمی عضو
از طرفی می دانیم حداکثر مقاومت فشاری عضو در حالت استفاده از آرماتور عرضی به شکل تنگ بسته و دورپیچ برابر است با:

با توجه به اطلاعات داده شده، در حالت اول با استفاده از دورپیچ در حالت فشار – کنترل φ=0.75 بوده و داریم:

در حالت دوم با استفاده از تنگ موازی تغییر می کند ولی بار وارده ثابت و برابر همان مقدار حالت اول می باشد (تغییر نوع آرماتور عرضی در مقدار بار نهایی اعمالی بی تاثیر است)، اما نکته قابل توجه این است که در صورت استفاده از دورپیچ، ضریب کاهش مقاومت برابر 0.75 ولی با در نظر گرفتن تنگ های موازی این ضریب برابر 0.65 می باشد. در این صورت داریم:


بنابراین با تغییر نوع آرماتور عرضی ستون نسبت Su به Sr حداکثر برابر 1.19 خواهد شد و گزینه 2 صحیح است.
تذکر: دقت شود در صورتی که در این سوال مقطع در حالت انتقالی باشد، ضریب φ با توجه به مقدار کرنش نهایی مقطع در محدوده 0.65 الی 0.9 تغییر می کند، اما به دلیل اینکه حداکثر نسبت Sr/Su مورد سوال قرار گرفته است، یعنی حالت فشار خالص که دارای کوچکترین ضریب φ می باشد مورد نظر بوده است.
مثال: در ستون بتنی درجا ریخته شده غیر لرزه ای شکل زیر، حداکثر ظرفیت فشاری اسمی مقطع حدودا چه مقدار است؟ (میلگردهای اصلی از نوع S500 و بتن C35 می باشد).
1- 4332 2- 6190 3- 5261 4- 4952 کیلونیوتن

حل: مطابق رابطه فصل اول داریم:
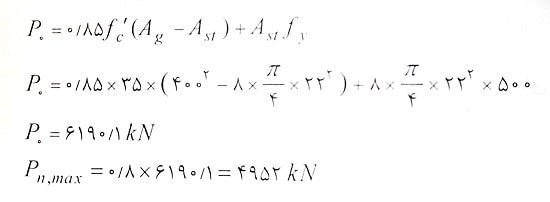
بنابراین گزینه 4 صحیح است.
مثال: یک ستون بتن آرمه با مقطع مربع شکل به بعد 500 mm را در نظر بگیرید. در این مقطع آرماتورهای طولی شامل 8φ20 بوده که با استفاده از یک تنگ بسته مربعی به قطر 10 mm در فواصل 200 میلی متری در ستون به کار رفته است. به این ستون بارهای محوری مرده 1800 kN و زنده 1400 kN بدون خروج از محوریت اعمال می گردد. با توجه به اطلاعات داده شده به سوالات زیر پاسخ دهید. (بتن از رده C30 و فولادها از رده S400 می باشند.)
الف) وضعیت ستون را تحت بارگذاری اعمالی بررسی کنید.
ب)بدون توجه به ضوابط آرماتورگذاری آیین نامه ای، حداقل مساحت آرماتورهای طولی چقدر باشد تا ستون از مقاومت کافی برخوردار باشد؟
حل: الف) با توجه به اینکه ستون تحت نیروی محوری خالص ناشی از بارها مختلف قرار گرفته است، لازم است رابطه زیر در خصوص مقاومت آن برقرار باشد:
![]()
با توجه به اینکه مقطع صرفا تحت نیروی محوری فشاری قرار دارد، بنابراین تمام آرماتورها تحت کرنش فشاری قرار گرفته و مقطع وضعیت فشار – کنترل دارد، لذا ضریب φ=0.65 در نظر گرفته می شود. از طرفی با توجه به وجود تنگ بسته در مقطع مقدار Pn,max=0.8P0 بوده، و داریم:
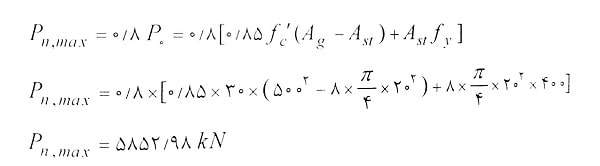
از طرفی با توجه به جدول بارگذاری ارائه شده فصل اول کتاب داریم:

همانطور که مشاهده می شود، مقطع از مقاومت کافی در برابر بارهای وارده برخوردار نمی باشد.
ب) همانطور که در قسمت اول مشاهده شد، مقطع ستون مورد نظر با توجه به آرماتورگذاری داده شده فاقد مقاومت لازم است. در این حالت با توجه به رابطه Pu≤φPn,max می توان مساحت آرماتورهای لازم را به صورت زیر محاسبه کنید:
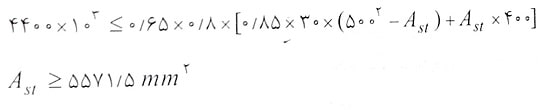
بنابراین با تعبیه 5571.5 میلی متر مربع آرماتور که تقریبا معادل 12φ25 است، می توان مقاومت مقطع را در برابر بارهای وارد تامین نمود.
البته باید توجه نمود که پس از محاسبه مساحت آرماتورهای مورد نیاز مقطع لازم است مقدار آن را با مقادیر حداقل و حداکثر آیین نامه ای کنترل کرده و در نهایت مقدار آرماتور مجاز در مقطع را تعیین نمود که با این مفاهیم در بخش های بعدی کاملا آشنا خواهید شد.
مثال: مقطع زیر برای یک ستون کوتاه مهار شده بتنی که تحت اثر نیروی محوری ناشی از بار مرده برابر 2200 kN و نیروی محوری فشاری ناشی از بار زنده برابر 1400 kN قرار دارد، طرح شده است. کدام عبارت در رابطه با طراحی مقطع ستون صحیح است؟ (بتن C25 و فولاد S400).
1) مقطع ستون به علت کمبود مقاومت فشاری قابل قبول نیست.
2)مقطع ستون به علت فاصله غیر مجاز آرماتورهای طولی قابل قبول نیست.
3)مقطع ستون به علت نامناسب بودن فاصله آرماتورهای عرضی قابل قبول نیست.
4)مقطع ستون قابل قبول است.

حل:
حداکثر مقاومت فشاری اسمی مقطع با توجه به این که ستون دارای تنگ های عرضی می باشد، برابر است با:

در ادامه بار نهایی وارد بر این مقطع نیز با توجه به جدول ترکیب بار فصل اول کتاب برابر است با:

از طرفی مقطع در حالت بار محوری خالص به صورت فشار – کنترل بوده و ضریب φ=0.65 در نظر گرفته می شود.

بنابراین مقطع به لحاظ کمبود مقاومت فشاری قابل قبول نبوده و بنابراین گزینه 1 صحیح است.
تعیین محل مرکز پلاستیک
مطابق آنچه در بخش قبل گفته شد، با ضوابط تحلیل ستونی که تحت اثر بار محوری خالص قرار گرفته است، آشنا شدیم. حال سوال اساسی این است که چه ستونی تحت بار محوری خالص قرار دارد؟
در پاسخ به این سوال باید بگوییم تقریبا هیچ ستونی در واقعیت تحت بار محوری خالص قرار ندارد، بلکه همواره اندکی لنگر خمشی نیز در اثر خروج از مرکزیت بار به صورت تصادفی یا واقعی بر ستون اعمال شده و از طرفی شرایط اعمال بار متمرکز محوری خالص نیز مگر در حالات خاص آزمایشگاهی وجود ندارد.
اما با توجه به اینکه به صورت تئوری این حالت قابل تصور است، بنابراین شرح این مطلب به لحاظ محاسباتی و همچنین در آزمون های نظام مهندسی حائز اهمیت می باشد.
به منور اینکه یک ستون تحت بار محوری خالص قرار بگیرد، لازم است بار محوری به صورت متمرکز و دقیقا بر محل مرکز پلاستیک مقطع اعمال گردد، در این شرایط خروج از مرکزیت محوریت نیروی اعمالی برابر صفر بوده و هیچ گونه لنگر خمشی به مقطع ستون اعمال نمی گردد.
تعیین مرکز پلاستیک
مرکز پلاستیک مقطع محلی است که چنانچه در حالت نهایی نیروی محوری بر این نقطع اعمال شود، هیچ گونه لنگر خمشی در مقطع ایجاد نشده و تمام مقطع تحت کرنش یکسان قرار گیرد. در واقع این نقطه محل برآیند نیروهای فشاری حاصل از بتن و آرماتورها می باشد.
برای تعیین محل مرکز پلاستیک مقطع ستون کافی است از رابطه زیر که در خصوص یک مقطع مستطیل شکل فرضی با دو ردیف آرماتور در دو وجه مقطع می باشد، استفاده نمایید.
لنگر ناشی از آرماتورهای A’s و As حول وجه AB+ لنگر ناشی از نیروی بتن حول وجه P0* Xp=AB

در حالت کلی برای پیدا کردن محل مرکز پلاستیک در یک شکل دلخواه مانند یک ستون L شکل گام های زیر را طی می کنیم:
گام اول: مبدا مورد نظر را مشخص کنید. برای این منظور کافی است ببینید در سوال مرکز پلاستیک تا کدام وجه خواسته شده و یا مبدا مورد نظر در کدام نقطه قرار گرفته است؟ به طور مثال در مقطع شکل زیر فاصله مرکز پلاستیک تا وجه فوقانی مورد نظر بوده، به همین دلیل مبدا Yp در وجه فوقانی در نظر گرفته شده است.
گام دوم: در این مرحله برای اطمینان از صحت محاسبه نیروهای مقطع نمودار تنش ها را در جهت مبدا انتخابی رسم می کنیم. پس از تمرین کافی و تحلیل مقاطع مختلف، نمودار تنش ها در ذهن شما نقش بسته و الزامی به رسم نمودار نخواهید داشت.

گام سوم: در این مرحله کافی است رابطه زیر را محاسبه کنید:

توجه کنید در مقاطعی که ترکیبی از چند شکل ساده هستند (مثل مقطع L شکل) کافی است مقطع را به شکل های هندسی ساده تقسیم کرده و نیرو و بازوی لنگر در هر قسمت نسبت به لبه مورد نظر را محاسبه نمایید. به طور مثال مقطع L شکل فوق به دو مستطیل 1 و 2 تقسیم شده است. برای درک بهتر به نحوه محاسبه نیروها و بازوی لنگر هر قسمت توجه کنید.

چند نکته کاربردی:
در تعیین محل مرکز پلاستیک ستون های مختلف به موارد زیر توجه کنید:
1)در صورتی که مقطع ستون دارای دو محور تقارن باشد، محل مرکز پلاستیک بر روی محل تقاطع محورهای تقارن منطبق می باشد. در این صورت نیازی به هیچ محاسبه خاصی وجود نداشته و مرکز پلاستیک براسا هندسه مقطع بدست می آید.
2)در مقاطعی که دارای یک محور تقارن هستند، مرکز پلاستیک مقطع در یک راستا بر محور تقارن قرار داشته و در راستای دیگر باید موقعیت آن مطابق محاسبات فوق تعیین شود.
3)در مقاطع فاقد محور تقارن، محل مرکز پلاستیک در دو راستا باید براساس محاسبات گفته شده بدست آید.
در ادامه با چند مثال بر روی مفاهیم مرکز پلاستیک کاملا مسلط خواهیم شد.
مثال: به یک ستون بتن ارمه با مقطع نشان داده در شکل زیر نیروی محوری Pu بر روی وجه کناری مقطع به صورت نشان داده شده اعمال شده و این نیرو مقطع را به وضعیت نهایی می رساند. چنانچه مصالح مصرفی C30 و S400 باشد، با توجه به سایر مشخصات ارائه شده بر روی شکل، مقدار لنگر خمشی وارد بر ستون در این حالت چند kN.m خواهد بود؟ ابعاد نشان داده شده در شکل بر حسب میلی متر می باشند.

حل: به شکل نشان داده شده و موقعیت بار اعمالی به ستون دقت کنید. لنگر خمشی ناشی از بارگذاری برابر فاصله محل اعمال بار تا مرکز پلاستیک ستون می باشد.
همانطور که احتمالا حدس زده اید، با توجه به اینکه بار بر وجه کناری مقطع اعمال شده است، بنابراین برای حل این سوال کافی است فاصله مرکز پلاستیک را تا وجه کناری مقطع بدست آوریم:
به علت عدم تقارن آرماتورگذاری، برای محاسبه مرکز پلاستیک نسبت به لبه سمت راست داریم:
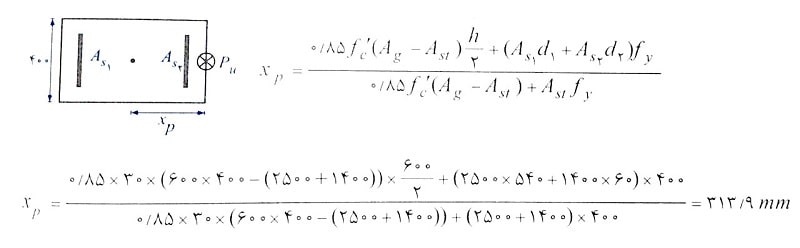
e مقدار خروج از مرکزیت نیرو نسبت به مرکز پلاستیک.
Mu=Pu.e Mu=Pux313x10-3
نکته تستی: همانطور که مشاهده شد، مقدار فاصله مرکز پلاستیک بزرگتر از h/2=300 mm بدست آمده است. آیا می توانستید پیش از محاسبه دقیق این موضوع را حدس بزنید؟ در این سوال مقطع داده شده متقارن ولی آرماتورگذاری نامتقارن است، بنابراین بدیهی است که مرکز پلاستیک مقطع به سمت آرماتور با مساحت بیشتر یعنی As1 متمایل گردد. با توجه به این نکته می توانیم حدس بزنیم که مقدار لنگر خمشی کمی بیشتر از 0.3Pu خواهد بود و گزینه های 1 و 2 حذف می شوند.
مثال: ستون بتن آرمه با مقطع نشان داده شده در شکل زیر را در نظر بگیرید. با توجه به مشخصات ارائه شده محل مرکز پلاستیک این مقطع در راستای قائم در چه فاصله ای از وجه تحتانی قرار دارد؟ مصالح مصرفی C30 و S400 در نظر گرفته می شود.
As2=2000 mm2 و As1=1500 mm2 ابعاد مشخص شده در شکل بر حسب میلی متر هستند.

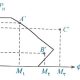
حل: مقطع نشان داده شده نامتقارن است پس برای تعیین مرکز پلاستیک آن با استفاده از روش گام به گام و تقسیم مقطع به 3 مستطیل ساده داریم:
گامل اول: با توجه با اینکه مبدا مورد نظر در سوال مشخص شده است بنابراین مبدا در دو وجه تحتانی مقطع قرار دارد.
گام دوم: رسم نمودار تنش های ایجاد شده در بتن و فولاد در راستای مبدا انتخابی.

گام سوم: با توجه به تبدیل مقطع به سه مستطیل ساده داریم:
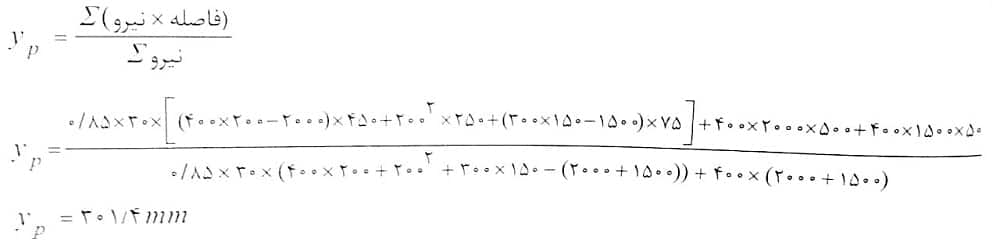
بنابراین گزینه 1 صحیح است.



دیدگاه خود را ثبت کنید
تمایل دارید در گفتگوها شرکت کنید؟در گفتگو ها شرکت کنید.