ستون تحت اثر بار محوری و لنگر خمشی یک طرفه

ستون تحت اثر بار محوری و لنگر خمشی یک طرفه

در بخش قبل خواندیم که اگر نیروی محوری بر مرکز پلاستیک ستون اعمال شود، هیچ گونه لنگر خمشی در مقطع به وجود نخواهد آمد.

اما همانطور که گفته شد این حالت بسیار نادر بوده و در اغلب سازه های بتن آرمه به علاوه نیروی محوری، لنگر خمشی نیز به طور همزمان بر ستون اعمال می گردد. از جمله مهمترین علل ایجاد این امر می توان به موارد زیر اشاره کرد:

1)شرایط اجرا شده در یک سازه با شرایط در نظر گرفته شده برای آن در هنگام طراحی معمولا متفاوت استبه عبارتی مقداری خطا در هنگام اجرای سازه وجود دارد.

2)بارگذاری نامتقارن بر روی کف باعث ایجاد لنگر خمشی در ستون می شود.

3)حرکت بارهای زنده بر روی سازه باعث تغییر محل اعمال بار و ایجاد لنگر در ستون می شود.

4)لنگرهای خمشی به طور مستقیم ناشی از بارگذاری های خارج از مرکز و یا نیروهای جانبی در ستون ایجاد می شوند.

با توجه به موارد فوق، ستون ها علاوه بر بار محوری، تحت لنگر خمشی نیز قرار داشته و تحلیل آنها باید با در نظر گرفتن هر دوعامل انجام گردد.

در ادمه بحث می خواهیم شیوه تحلیل ستون تحت اثر نیروی محوری و لنگر خمشی یک طرفه را شرح داده و به بررسی انواع شکست در ستون ها بپردازیم.

ستون تحت نیروی محوری و لنگر خمشی یک طرفه

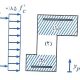
به مقطع ستون بتن آرمه شکل زیر، نیروی محوری P و لنگر خمشی M وارد می شود، به طوری که این بارگذاری ستون را به وضعیت نهایی رسانده است.

در این حالت مقدار کرنش در بحرانی ترین تار فشاری بتن یعنی BC به کرنش Ԑ_cu می رسد. در ستون ها نیز دقیقا مشابه آنچه در فصل خمش گفته شد، نمودار تنش ها با استفاده از بلوک توزیع تنش مستطیلی به صورت زیر رسم می شود:

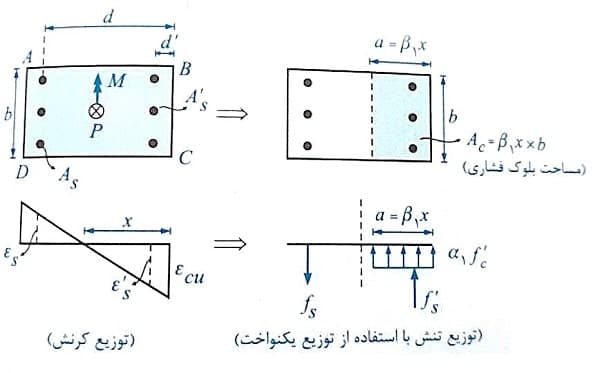
حال فرض کنید می خواهیم مقادیر P و M (یا همان P و e یعنی خروج از محوریت که معادل لنگر خمشی  اعمالی است) را که با تاثیر همزمان بر ستون باعث گسیختگی آن می شوند، تعیین کنیم. برای این منظور ستون باید در حالت نهایی تحلیل شود.

بررسی چند سوال

سوال 1: با فرض مشخص بودن مقدار x در شکل صفحه قبل، کرنش و تنش ایجاد شده در فولادهای A’_s و A_s را بدست آورید.

پاسخ: در صورتی که مقادیر کرنش در فولادهای فشاری و کششی (Ԑ_s’ و Ԑ_s) مشخص شده و با کمک آنها مقادیر تنش در فولادها (f’_s و f_s) به صورت زیر بدست می آید:

سوال 2: مقدار مقاومت فشاری محوری اسمی ستون (P_n) را چگونه می توان بدست آورد؟

پاسخ:

در فصل خمش مرتبا بیان می کردیم که براساس رابطه تعادل، نیروی کششی برابر نیروی فشاری بوده و با کمک این معادله ساده، مسائل زیادی تحلیل شد؛ اما در ستون ها این موضوع کمی متفاوت است.

در اینجا، تفاضل نیروی فشاری و کششی، برابر نیروی محوری فشاری وارد بر مقطع می باشد (در واقع در فصل خمش به دلیل صفر بودن نیروی محوری، نیروی کششی مساوی نیروی فشاری بود.)

دقت شود در اینجا نیز برای تعیین نیروی فشاری بتن، مشابه فصل خمش از توزیع تنش مستطیلی استفاده کرده، بنابراین با توجه به توضیحات و شکل رسم شده در ابتدای بحث، مقدار مقاومت فشاری محوری اسمی ستون به صورت زیر بدست می آید:

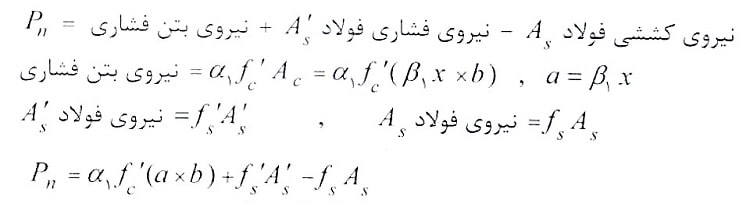
سوال 3: مقدار مقاومت خمشی اسمی ستون چگونه محاسبه می شود؟

پاسخ: در صورتی که لنگر اعمالی با یک نیروی خروج از محور معادل سازی شود، مقدار لنگر را می توان از حاصلضرب نیرو در خروج از محوریت نسبت به مرکز پلاستیک ستون  محاسبه نمود.

در این صورت با محاسبه لنگر اجزای داخلی نسبت به  مرکز پلاستیک مقطع، می توان مقدار مقاومت خمشی  اسمی ستون را محاسبه کرد. براین اساس در مقطع شکل زیر با معلوم بودن محل مرکز پلاستیک  (X_p) داریم:

همانطور که در دور رابطه بالا مشاهده می شود، مقدار لنگر نهایی وارد بر مقطع در لحظه نهایی، به پارامتر X وابسته است. به عبارت دیگر برای هر مقدار از X، یک ترکیب از P و M وجود دارد که باعث رسیدن ستون به حالت نهایی می شود. بنابراین در یک ستون، بی نهایت ترکیب از نیرو و لنگر وجود دارد که حالت نهایی را ایجاد کرده و ستون را در آستانه گسیختگی قرار می دهد.

برای طراحی ستون، این مقادیر P و M را بر روی یک نمودار به نام اندرکنش بار محوری-لنگر خمشی نشان می دهند که در قسمت بعدی صحبت می کنیم. بریم سراغ حل تمرین و مثال.

مثال: در ستونی با مقطع زیر، وضعیت کرنش ها در حالت نهایی چنان است که تنش در میلگرد کششی A_s صفر می باشد. بگویید کدامیک از گزینه های زیر به مقادیر نیروی محوری و لنگر خمشی اسمی این ستون نزدیکتر است؟

A’_s=A_s=1200 mm² , f’_c=20Mpa , f_y=400 Mpa

حل: با توجه به اینکه تنش در آرماتورهای کششی A_s صفر است، بنابراین این آرماتورها بر روی محوری خنثی قرار گرفته اند و عملا طراح با این موضوع مقدار پارامتر x را مشخص کرده است. با مشخص بودن مقدار x، مقدار Ԑ_s^’ به صورت زیر محاسبه می گردد:

در ادامه مقاومت فشاری محوری اسمی ستون، با استفاده از رابطه گفته شده بالا به صورت زیر بدست می آید:

با توجه به اینکه مقطع دارای دو محور تقارن است، مرکز سطح و مرکز پلاستیک بر هم منطبق بوده و بنابراین مقاومت خمشی اسمی مقطع برابر است با:

بنابراین گزینه 4 صحیح است.

مثال: با توجه به اطلاعات ارائه شده در مثال بالا، حداکثر مقدار نیروی محوری و لنگر خمشی که می توان به صورت همزمان به ستون اعمال کرد را محاسبه کنید.

حل: می دانیم در ستون ها حداکثر نیور و لنگر خمشی قابل اعمال به صورت زیر بدست می آید:

P_u≤φP_n

M_u≤φM_n

با توجه به اینکه تنش در میلگرد کششی این مقطع برابر صفر است، یعنی در لحظه نهایی Ԑ_t=0 بوده، بنابراین به دلیل اینکه Ԑ_t<Ԑ_y است، مقطع به صورت فشار-کنترل در نظر گرفته شده و ضریب φ با توجه به مستطیلی بودن مقطع و استفاده از تنگ های موازی در آن برابر 0.65 در نظر گرفته می شود.

در  این صورت حداکثر نیروی محوری و لنگر خمشی قابل اعمال به ستون برابر است با:

P_u≤0.65×360.1           P_u≤234.1 ton

M_u≤0.65×33.5            M_u≤21.8 ton.m

توجه شود در صورتی که هر دو رابطه بالا به طور همزمان برقرار باشد، ستون به حالت نهایی نرسیده و گسیخته نمی شود. اما اگر به طور مثال P_u=250 ton و M_u=10 ton.m باشد، برای تحلیل گسیختگی ستون باید به نمودار اندرکنش بار محوری – لنگر خمشی مراجعه کرد که در ادامه آن را شرح می دهیم.

منحنی اندرکنش بار محوری – لنگر خمشی

همانطور که در قسمت قبل بررسی کردیم، شکست ستون به ازای مقادیر مختلفی از نیروی محوری و لنگر خمشی می تواند رخ دهد.

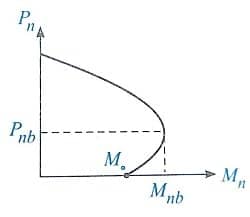
اگر مقادیر مختلف نیروی محوری و لنگر خمشی وارد بر ستون که باعث خرابی آن می شود را در یک نمودار رسم کنیم، منحنی اندرکنش نیرو – لنگر برای ستون بدست می آید.

فرم کلی این نمودار به صورت زیر است:

در این منحنی سه نقطه مشخص است که مفهوم آنها برای ما بسیار حائز اهمیت است. در ادامه با بررسی چند سوال به بررسی نمودار اندرکنش می پردازیم.

بررسی چند سوال

سوال 1: اصلی ترین مطلبی که از نمودار اندرکنش ستون برداشت می شود چه موضوعی است؟

پاسخ: برای بررسی این سوال به چند نکته زیر توجه کنید:

1)منحنی اندرکنش ستون و به عبارت بهتر، نقاطی که روی منحنی قرار می گیرند، نشان دهنده ترکیب های مختلف نیروی محوری و لنگر خمشی هستند که حالت مقاومت اسمی ستون (حالت نهایی) را نشان می دهند. با در نظر گرفتن ضریب کاهشی φ در مقادیر واقع بر روی نمودار، ظرفیت نهایی مقطع و حالت گسیختگی مقطع بدست خواهد آمد.

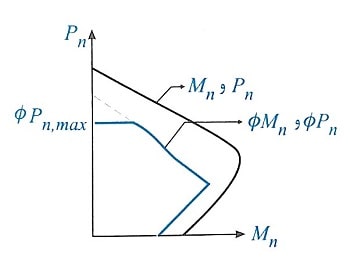
در این صورت می توان نمودار مقطع را به صورت ساده و با لحاظ ضریب کاهنده φ به منظور نمایش حالت گسیختگی به صورت منحنی داخلی در نمودار فوق در نظر گرفت.

توجه شود قسمت ثابت در ابتدای نمودار کاهش یافته برابر مقدار P_nmax و معرف در نظر گرفتن ضرایب اطمینان آیین نامه در شاریط بار محوری خالص می باشد.

2)نقاطی که داخل منحنی قرار می گیرند، بیانگر ترکیبات مختلف نیروی محوری و لنگر خمشی هستند که تحت اثر آنها ستون از مقاومت کافی برخوردار بوده و لذا با اعمال آنها به حد نهایی نمی رسد.

3)نقاطی که خارج از منحنی قرار می گیرند، نشان دهنده ترکیبات نیروی محوری و لنگر خمشی است که بیشتر از حد مقاومت ستون بوده و ستون پیش از رسیدن به مقادیر آنها گسیخته شده است.

با توجه به این توضیحات در مورد سه ستون که در موقعیت های A’، B’ و C’ قرار دارند، با توجه به نمودار φP_n و φM_n می توان گفت:

نقطه A’: تحت ترکیب M₁ و P₁ ستون در آستانه خرابی قرار می گیرد (روی نمودار اندرکنش).

نقطه B’: تحت ترکیب M₂ و P₂ ستون ایمن است (داخل منحنی اندرکنش).

نقطه C’: پیش از رسیدن به ترکیب M₃ و P₃ ستون خراب شده است (خارج از منحنی اندرکنش).

بنابراین ناحیه داخل منحنی اندرکنش، عملا ناحیه امن محسوب شده و تا زمانی که نیرو و لنگر وارد بر ستون در این ناحیه قرار بگیرد، ستون گسیخته نمی شود.

سوال 2: در مورد نقطه A از منحنی اندرکنش مقابل، چه اظهار نظری می توان کرد؟

پاسخ: در نقطه A، لنگر خمشی برابر صفر بوده و ستون فقط دارای مقاومت محوری خالص و بدون وارد شدن لنگر است. به عبارت بهتر در این نقطه بار محوری در مرکز پلاستیک ستون وارد شده و خروج از مرکزیت آن صفر است. در این حالت در لحظه نهایی، کرنش در تمام تارهای مقطع برابر Ԑ_cu بوده و نیروی محوری وارد بر ستون همان P₀ است (حالت بار محوری خالص).

تذکر: همانطور که در شکل فوق مشاهده می کنید، در این نقطه از نمودار اولا تمام فولادهای موجود در مقطع تحت فشار قرار دارند و ثانیا با توجه به اینکه کرنش آنها برابر Ԑ_cu بوده و Ԑ_cu>Ԑ_y است، تنش ایجاد شده در آن ها برابر f_y می باشد.

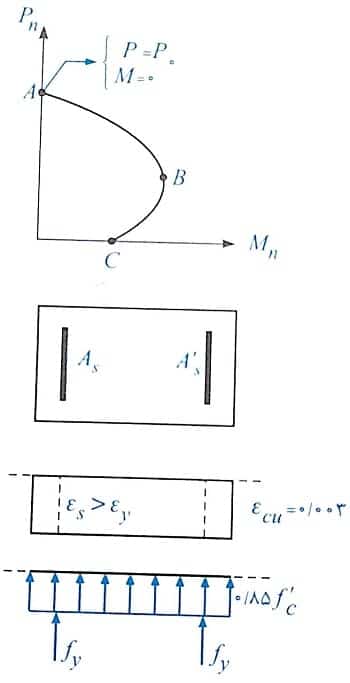
سوال 3: در مورد نقطه C از منحنی اندرکنش مقابل چه اظهار نظری می توان کرد؟

پاسخ: در نقطه C، نیروی محوری برابر صفر بوده و ستون تنها دارای مقاومت خمشی می باشد. بنابراین رفتار ستون در این نقطه، دقیقا مانند یک تیر تحت خمش خالص است.

نقطه C: P_n=0 , M_n=M₀

سوال 4: نقطه B حالت شکست بسیار مهمی برای یک ستون محسوب شده و نقطه شکست بالانس نام دارد. ویژگی های این نقطه از نمودار بررسی کنید. 

پاسخ: در نقطه B از نمودار، ترکیب نیروی محوری و لنگر خمشی به گونه ای است که اولا در قسمتی از مقطع تار کششی ایجاد شده و ثانیا درست در لحظه ای که کرنش در دورترنی تار بتن فشاری به Ԑ_cu برسد، کرنش در دورترین ردیف فولاد کششی به Ԑ_y می رسد. این وضعیت از شکست در یک ستون، شکست بالانس نامیده می شود. ویژگی های این نقطه از نمودار اندرکنش عبارت است از:

1)با توجه به نمودار اندرکنش زیر، در حالت بالانس بیشترین لنگر خمشی توسط ستون تحمل می شود (این موضوع یعنی در حالتی که ستون تحت لنگر خمشی خالص قرار دارد، حداکثر لنگر خمشی را تحمل نمی کند).

2)x_b دقیقا مانند فصل خمش، به سادگی از روی نمودار توزیع کرنش و با کمک تشابه مثلث ها بدست آمده و مقدار آن عبارت است از:

3)با محاسبه x_b برای مقطع، مقادیر Ԑ^’_s و f^’_s به سادگی محاسبه شده و با استفاده از آن مقاومت فشاری محوری اسمی در حالت بالانس (P_nb) و مقاومت خمشی اسمی در حالت بالانس (M_nb) قابل محاسبه است. دقت شود که در حالت بالانس فولاد A_s جاری شده و تنش آن برابر f_y است.

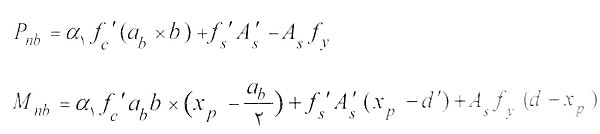
4)همانطور که در ابتدای بخش گفته شد، نیروی محوری و لنگر خمشی وارد بر مقطع را می توان به صورت یک نیروی با محوریت خروج از مرکزیت معادل در نظر گرفت. در این صورت خروج از مرکزیت مربوط به حالت بالانس، e_b، برابر با eb=Mnb/Pnb  در نظر گرفته می شود.

C.P مرکز پلاستیک مقطع.

همانطور که در فصل اول از رابطه مورد نظر برای محاسبه مقاومت محوری خالص ستون ها خواندیم، مقدار تنش فشاری بتن برابر 0.85f^’_c در نظر گرفته شده در حالیکه تحت ترکیب نیروی محوری و لنگر خمشی، مقدار این تنش مشابه فصل خمش و برابر α₁f^’_c در نظر گرفته شده است.

باید توجه نمود علیرغم اینکه نباید تفاوتی در خصوص مقدار تنش در این دو حالت وجود داشته باشد، آیین نامه به دلیل ارجاع حالت دوم به محاسبات فصل خمش، از این موضوع غفلت نموده است.

البته باید توجه نمود این اختلاف در خصوص بتن های با مقاومت بیشتر از 55 مگاپاسکال که در آنها مقدار α₁ کوچکتر از 0.85 است، مطرح می شود؛ که این نوع بتن های پر مقاومت نیز در ساختمان های متداول کاربرد چندانی ندارند.

مطلب بعدی: انواع شکست ستون

پیج اینستاگرام سیویل 2