طراحی اعضای تحت اثر ترکیب نیروها
طراحی اعضای تحت اثر ترکیب نیروها
در سازه های فولادی به ندرت اعضایی وجود دارند که صرفا تحت تاثیر یکی از نیروهای کششی، فشاری و یا لنگر خمشی قرار داشته باشند و غالبا اعضای سازه های فولادی تحت تاثیر ترکیبی از نیروهای محور، برشی و لنگر خمشی هستند.
به طور مثال اگر یک عضو فولادی تحت تاثیر همزمان نیروی محوری و لنگر خمشی قرار بگیرد، تیر-ستون نامیده می شود.
طراحی تیر-ستون تحت اثر لنگر خمشی و نیروی محوری کششی
در یک تیر – ستون تحت اثر توام نیروی محوری کششی و لنگر خمشی، از یک طرف موضوع کمانش کلی مطرح نبوده و از سوی دیگر با توجه به کوچک شدن مساحت ناحیه فشاری، پتانسیل کمانش موضعی و کمانش پیچشی – جانبی در بال فشاری کاهش می یابد.
این اعضاء باید در تمام طول خود رابطه زیر را برآورده نمایند:
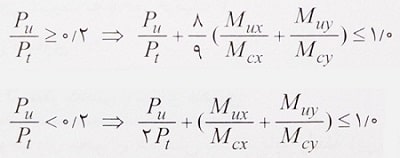
که در آن:
Pu: مقاومت کششی مورد نیاز
ΦPn=Pt: مقاومت کششی طراحی
Φ: ضریب کاهش مقاومت در کشش (بسته به نوع گسیختگی کششی برابر 0.9 یا 0.75 است)
Mux: مقاومت خمشی مورد نیاز نسبت به محوری قوی x
Muy: مقاومت خمشی مورد نیاز نسبت به محور ضعیف y
ΦMnx=Mcx: مقاومت خمشی طراحی نسبت به محور قوی x
ΦMny=Mcy: مقاومت خمشی طراحی نسبت به محور ضعیف y
Φ: ضریب کاهش مقاومت برای خمش مساوی 0.9
تبصره: برای اعضای دارای دو محور تقارن تحت اثر همزمان لنگر خمشی و نیروی محوری کششی، ضریب اصلاح کمانش پیچشی – جانبی (Cb) می تواند با ضریب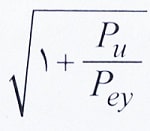 افزایش یابد که در آن Pey از رابطه زیر تعیین می گردد:
افزایش یابد که در آن Pey از رابطه زیر تعیین می گردد:
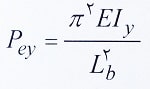
پارامترهای مورد استفاده در رابطه فوق عبارتند از:
E: مدول الاستیسیته فولاد
Lb: فاصله مهارهای جانبی در طول عضو
Iy: ممان اینرسی حول محور ضعیف y
طراحی تیر – ستون تحت اثر لنگر خمشی و نیروی محوری فشاری
به منظور طراحی تیر – ستون تحت اثر توام لنگر خمشی و نیروی فشاری به صورت زیر عمل می شود:
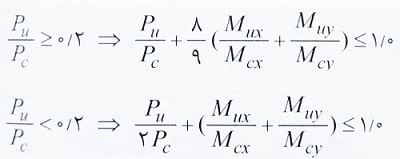
پارامترهای مورد استفاده در روابط فوق عبارتند از:
Pu: مقاومت فشاری مورد نیاز
ΦPn=Pc: مقاومت فشاری طراحی
Φ: ضریب کاهش مقاومت در فشار مساوی 0.9
Mux: مقاومت خمشی مورد نیاز نسبت به محور قوی x
Muy: مقاومت خمشی مورد نیاز نسبت به محور ضعیف y
ΦMnx=Mcx: مقاومت خمشی طراحی نسبت به محور قوی x
ΦMny=Mcy: مقاومت خمشی طراحی نسبت به محور ضعیف y
Φ: ضریب کاهش مقاومت برای خمش مساوی 0.9
طراحی مقاطع نامتقارن تحت اثر لنگر خمشی و نیروی محوری
مقاطع نامتقارن اگر تحت لنگر خمشی و نیروی محوری همزمان باشند، باید رابطه زیر برقرار شود:
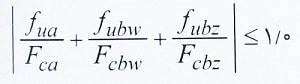
پارامترهای مورد استفاده در رابطه فوق عبارتند از:
fua: تنش محوری مورد نیاز
Fca: تنش محوری طراحی طبق الزامات گفته شده در قسمت های قبلی برای اعضای کششی و اعضای فشاری
fubz, fubw: تنش های خمشی مورد نیاز
Fcbz,Fcbw: تنش های خمشی طراحی مطابق روابط 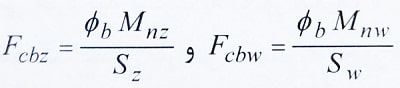
w: زیرنویس مربوط به خمش حول محور اصلی قوی
z: زیرنویس مربوط به خمش حول محور اصلی ضعیف
طراحی مقاطع مستطیلی توخالی تحت اثر ترکیب پیچش، خمش، برش و نیروی محوری
هرگاه مقاومت پیچشی مورد نیاز (Tu) کمتر یا مساوی 20 درصد مقاومت پیچشی طراحی (ΦTn) باشد، در این صورت پیچش در ترکیب با خمش، برش و نیروی محوری قابل صرف نظر بوده و اثر توام خمش و نیروی محوری تعیین می گردد.
اما چنانچه مقاومت پیچشی مورد نیاز (Tu) بیشتر از 20 درصد مقاومت پیچشی طراحی (ΦTn) باشد، در این صورت اثر توام پیچش، خمش، برش و نیروی محوری از رابطه زیر تعیین می شود.
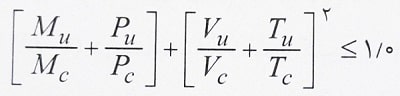
پارامترهای استفاده شده در رابطه فوق:
Pu: مقاومت محوری مورد نیاز Pc: مقاومت محوری طراحی مساوی ΦPn
Mu: مقاومت خمشی مورد نیاز Mc: مقاومت خمشی طراحی مساوی ΦMn
Vu: مقاومت برشی مورد نیاز Vc: مقاومت برشی طراحی مساوی ΦVn
Tu: مقاومت پیچشی مورد نیاز Tc: مقاومت پیچشی طراحی مساوی ΦTn
مثال: یک ستون با مقطع قوطی شکل به صورت زیر، تحت اثر همزمان نیروی محوری فشاری و لنگر خمشی دو محوره قرار دارد. اگر مقادیر این اثرات و همچنین مقدار ظرفیت های طراحی این مقطع به صورت زیر باشد، حداقل مقدار ظرفیت خمشی مقطع حول محور ضعیف تقریبا چند کیلونیوتن – متر باشد تا این ستون از نظر مقاومتی مشکلی نداشته باشد؟
نیروی فشاری وارد بر ستون = 2500kN ظرفیت فشاری طراحی = 6500kN
لنگر خمشی حول محور قوی = 350kN.m ظرفیت خمشی طراحی حول محور قوی = 820kN.m
لنگر خمشی حول محور ضعیف = 85kN.m ظرفیت خمشی طراحی حول محور ضعیف= ؟
1- 250 2- 290 3- 320 4- 360
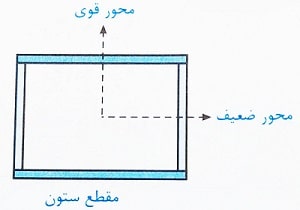
حل: برای اعضای با یک یا دو محور تقارن (مانند مقطع مورد بحث در این تست) که تحت اثر همزمان لنگر خمشی و نیروی محوری فشاری قرار دارند، اثر توام لنگرها و نیروی محوری به صورت زیر در نظر گرفته می شود:
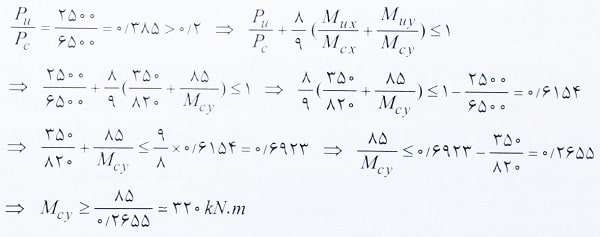
بنابراین گزینه 3 صحیح است.
مثال: در طراحی یک تیر اگر ΦMnx و ΦMny ظرفیت های خمشی مقطع ( ΦMny>ΦMnx ) و Mux و Muy لنگرهای نهایی ضریب دار یک مقطع باشند، کنترل مقطع برابر با رابطه زیر است:

حل: در این تیر بحثی از نیروی محوری نشده و لذا Pu=0 می باشد. داریم:
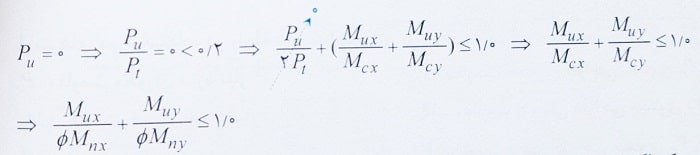
در نتیجه می توان گفت که اگر مقطعی تحت لنگر دو محوره قرار گیرد، باید مجوع نسبت لنگر نهایی موجود به لنگر طرح در هر دو جهت به عدد یک محدود شود و لذا گزینه 3 صحیح است.
مثال: مقطع نشان داده شده در شکل زیر، تحت اثر توام لنگر خمشی و نیروی محور کششی قرار دارد. چنانچه لنگر خمشی وارد بر مقطع حول محور x برابر 40kN.m باشد، حداکثر ظرفیت خمشی قابل تحمل توسط مقطع تقریبا چند کیلونیوتن است؟ (Fy=240MPa)
1- 960 2- 1060 3- 1150 4- 2160
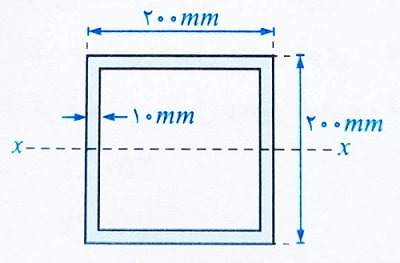
حل: برای بررسی اعضایی که تحت اثر همزمان لنگر خمشی و نیروی کششی قرار دارند باید طبق روابط گفته شده که به مقدار Pu/Pt وابسته است.
از آنجا که مقدار Pu را در اختیار نداریم و در واقع، دنبال محاسبه آن هستیم، ابتدا فرض می کنیم Pu/Pt<0.2 بوده و در انتها صحت آن را کنترل می کنیم.
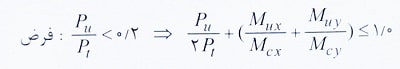
حال برای کنترل رابطه فوق، باید مقدار همه پارامترها (به جزء Pu) تعیین شده و سپس با استفاده از این رابطه مقدار Pu محاسبه شود.
دقت کنید که در این مقطع، لنگر خمشی فقط حول محور x است و Muy=0 است و در نتیجه نیازی به محاسبه Mcy نیست (هر چند به دلیل تقارن مقطع، Mcy=Mcx می باشد)
الف) محاسبه ظرفیت کششی مقطع: از آنجا که بحثی از وجود سوراخ در این مقطع نیست، ظرفیت کششی آن تنها ناشی از حالت حدی تسلیم می باشد و داریم:
![]()
ب) محاسبه ظرفیت خمشی مقطع: برای مقطع قوطی شکل، ظرفیت خمشی باید با توجه به قسمت قبلی بدست می آید.
حالت های حدی تسلیم، کمانش موضعی بال و کمانش موضعی جان باید بررسی شود. ابتدا کنترل فشردگی بال و جان مقطع را انجام می دهیم:
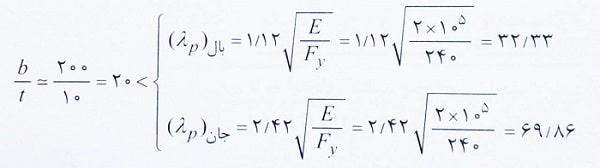
مشاهده می شود که بال و جان این مقطع فشرده است و نیازی به در نظر گرفتن کمانش موضعی بال و جان در تعیین ظرفیت خمشی نیست. حال تنها براساس حالت حدی تسلیم داریم:
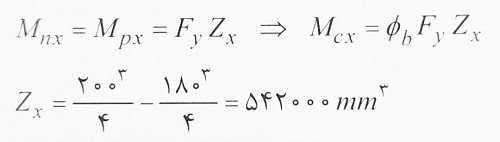
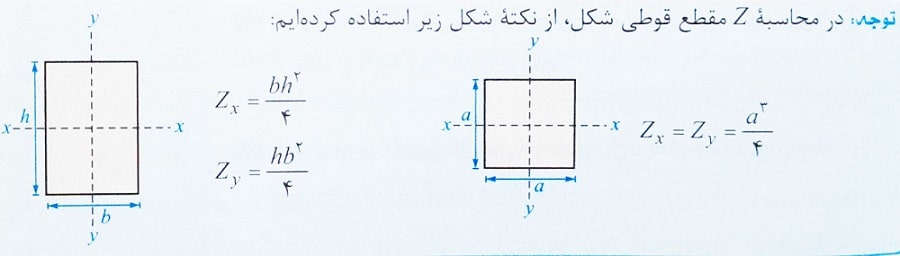
![]()
حال رابطه اندرکنش لنگر خمشی و نیروی محوری کششی را نوشته و داریم:
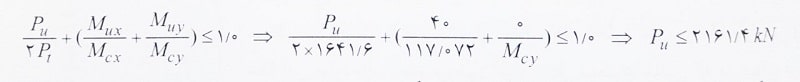
حال فرضی که در ابتدای حل تست داشتیم را بررسی می کنیم:
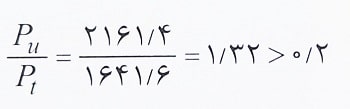
مشاهده می کنید که فرض Pu/Pt<0.2 برقرار نمی باشد. پس با انتخاب حالت Pu/Pt≥0.2 داریم:

مقدار جدید محاسبه شده برای Pu، شرط Pu/Pt≥0.2 را ارضاء می کند. پس آن را پذیرفته و در نتیجه گزینه 3 صحیح است.
طراحی تیرهای تحت اثر لنگ



دیدگاه خود را ثبت کنید
تمایل دارید در گفتگوها شرکت کنید؟در گفتگو ها شرکت کنید.