روش جایگزین برای طراحی دیوارهای لاغر
روش جایگزین برای طراحی دیوارهای لاغر
همانطور که قبلا با نحوه رفتار ستون های لاغر آشنا شدیم، همانطور که به خاطر دارید، در ستون های لاغر به دلیل ایجاد لنگرهای خمشی ثانویه، مقدار تغییر مکان ستون افزایش یافته و در صورتی که طراحی در برابر لنگرهای خمشی ثانویه به طور صحیح انجام نشده باشد، ممکن است گسیختگی ستون پیش از رسیدن به بارهای نهایی رخ دهد.
در مورد دیوارها، با توجه به نسبت های هندسی آن و نیروهای وارده، ممکن است لنگرهای خمشی و تغییر مکان های بیشتر از مقادیر اولیه پیش بینی نشده در دیوار ایجاد گردد.
در آیین نامه برای طراحی دیوارهای لاغر، به جای ضوابط مربوط به ستون های لاغر، روش جایگزینی برای طراحی دیوار در عملکرد خارج از صفحه پیشنهاد شده که در این قسمت به بررسی آن می پردازیم.
کنترل شرایط لاغری
اثرات لاغری در دیوارهایی که شرایط زیر در آنها برقرار باشد، می تواند مطابق روابطی که در این بخش به عنوان روش جایگزین شرح داده می شود محاسبه شود.
1- سطح مقطع در ارتفاع دیوار ثابت باشد، در واقع تغییر ضخامت و یا بازشو در دیوار وجود نداشته باشد.
2- رفتار خمشی خارج از صفحه دیوار به صورت کشش – کنترل باشد. یعنی تحت اثر لنگر خمشی اعمالی، کرنش دورترین آرماتورهای واقع در ناحیه کششی در لحظه نهایی، حداقل برابر εy+0.003 باشد.
3- حداقل مقدار ΦMn برابر Mcr باشد. در این خصوص Mcr لنگر خمشی ترک خوردگی دیوار می باشد که روش محاسبه آن مشابه آنچه در خصوص اعضای خمشی گفته شد می باشد.
4- مقدار Pu در مقطع وسط ارتفاع دیوار از 0.06f’cAfg بیشتر نباشد.
5- تغییر شکل خارج از صفحه محاسبه شده تحت اثر بارهای بهره برداری Δs با در نظر گرفتن اثرات P-Δ از lc/150 بیشتر نباشد. محاسبات Δs در انتهای این قسمت یاد می گیریم.
lc طول قائم از مرکز تا مرکز تکیه گاه دیوار می باشد.
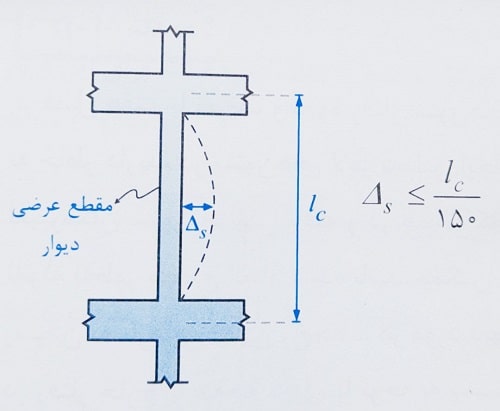
ضوابط مدلسازی دیوارهای لاغر
با اعمال اثر لاغری در دیوار در واقع می خواهیم حداکثر لنگر خمشی و متناسب با آن مقدار حداکثر تغییر مکان را تحت این لنگر بدست آوریم. برای همین منظور موارد زیر در هنگام مدلسازی دیوار در روش جایگزینی باید رعایت شود:
1- دیوار به صورت یک عضو با تکیه گاه های ساده در نظر گرفته می شود که تحت اثر بار محوری و بار جانبی گسترده یکنواخت خارج از صفحه قرار گرفته است. با توجه به این شرایط و مطابق شکل زیر مقدار حداکثر لنگر خمشی و تغییر مکان در وسط ارتفاع دیوار رخ می دهد.
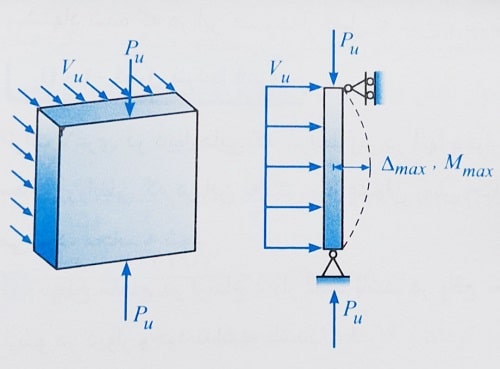
2- در مواردی که دیوار در ناحیه فوقانی تحت اثر بارهای متمرکز فوقانی قرار گرفته است، به منظور محاسبه حداکثر تنش محوری دیوار باید عرض ناحیه اعمال بار در ارتفاع دیوار به نحو مناسبی تعیین گردد. برای این منظور بارهای ثقلی متمرکز وارد شده به دیوار در بالای هر مقطع با فرض توزیع یکنواخت در عرضی برابر عرض ناحیه اعمال بار به علاوه عرضی در دو سمت با در نظر گرفتن شیب 1 به 2 (1 افقی و 2 قائم) لحاظ می شود. عرض کل بار در توزیع یکنواخت نباید از مقادیر زیر فراتر رود:
الف) فاصله بین بارهای متمرکز
ب) لبه های دیوار.
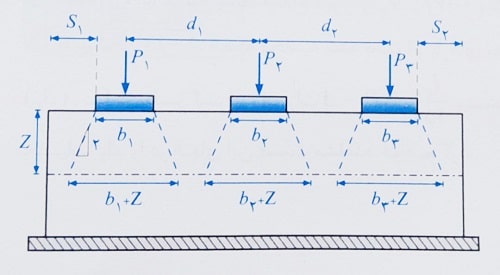
b1,b2,b3: عرض نواحی اعمال بار
Z: ارتفاع مقطع مورد نظر نسبت به سطح اثر اعمال بار
d1,d2: فواصل بارهای اعمالی
S1,S2: فواصل لبه محل اعمال نیرو نسبت به وجوه خارجی دیوار.
با توجه به شکل فوق، مقدار عرض بار در محل بار متمرکز P1 و در ارتفاع Z به صورت زیر کنترل می شود:
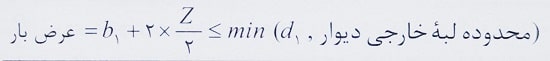
دقت شود در مورد بارهایی که در مجاورت لبه های خارجی دیوار که رسم توزیع 1 به 2 خارج از محدوده دیوار واقع می شود، مقدار عرض موثر بار به برکناری دیوار محدود می شود. به عنوان مثال در شکل بالا داریم:

در ادامه با حل مثال این موضوع را بررسی می کنیم.
مثال: یک دیوار بتن آرمه با ضخامت 250 میلی متر با طول 8 و ارتفاع 6 متر را در نظر بگیرید. مطابق تصویر زیر، به این دیوار بار متمرکز نهایی برابر 2000 کیلونیوتن از طریق تیری با عرض 400 میلی متر که در میانه طول دیوار واقع شده است، اعمال می شود. عرض بار در فاصله 3 متری از تکیه گاه این تیر در راستای قائم برای توزیع یکنواخت را محاسبه نمایید.
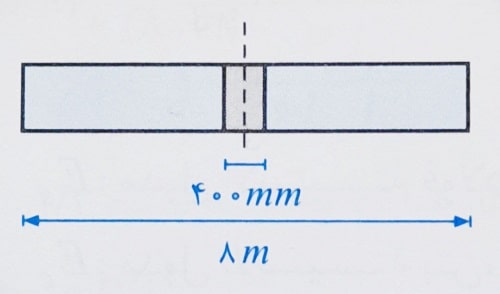
حل: عرض بار در فاصله 3 متری از تکیه گاه به صورت زیر محاسبه می شود:
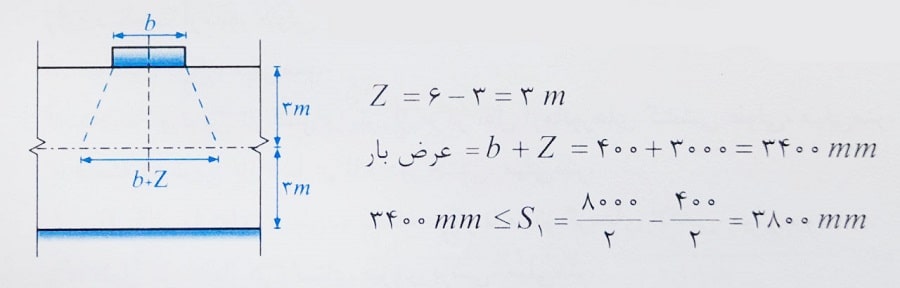
محاسبه لنگر ضریبدار در دیوارهای لاغر با روش جایگزین
برای محاسبه مقدار لنگر نهایی حداکثر دیوار تحت اثر بارهای محوری و لنگر خمشی، با توجه به تغییر شکل های ایجاد شده دو روش وجود دارد. یک روش براساس مقدار تغییر مکان های ایجاد شده و با تکرار محاسبات بدست آمده و روش دیگر به صورت مستقیم و براساس لنگر اولیه ایجاد شده در دیوار می باشد. روابط مورد استفاده در هر یک از این روش ها شرح داده می شود.
روش اول: روش تکرار محاسبات
در این حالت مقدار لنگر نهایی حداکثر وارد بر دیوار در وسط ارتفاع آن با استفاده از رابطه زیر بدست می آید:
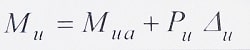
Mu: لنگر ضریبدار مقطع دیوار با لحاظ اثر P-Δ.
Mua: حداکثر لنگر ضریبدار در وسط ارتفاع دیوار ناشی از بارهای جانبی و بارهای محوری دارای خروج از مرکزیت ( دقت شود در این حالت اثر P-Δ در نظر گرفته نشده است)
Pu: نیروی محوری ضریبدار فشاری
Δu: مقدار تغییر مکان که با استفاده از رابطه زیر بدست می آید:
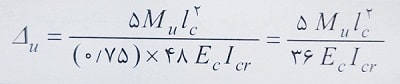
Icr: در رابطه فوق ممان اینرسی مقطع ترک خورده تبدیل یافته به بتن دیوار بوده که براساس رابطه زیر محاسبه می شود:
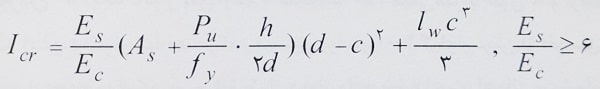
Es: مدول الاستیسیته فولاد، مگاپاسکال.
Ec: مدول الاستیسیته بتن، مگاپاسکال.
As: مساحت آرماتور طولی کششی، میلی متر مربع.
h: ضخامت دیوار، میلی متر.
d: فاصله دورترین تار فشاری بتن از مرکز ثقل آرماتورهای کششی طولی، میلی متر.
c: فاصله دورترین تار فشاری تا محور خنثی، میلی متر.
lc: طول قائم (ارتفاع) دیوار در فاصله مرکز تا مرکز گره های اتکایی، میلی متر.
lw: طول کل دیوار در راستای نیروی برشی، میلی متر.
تذکر: عمق محور خنثی برای محاسبه Icr در این حالت مشابه با حالت الاستوپلاستیک در تیرها انجام می شود. برای انجام این کار باید برای سطح مقطع فولاد از سطح مقطع موثر یعنی ترم زیر در رابطه Icr استفاده شود.
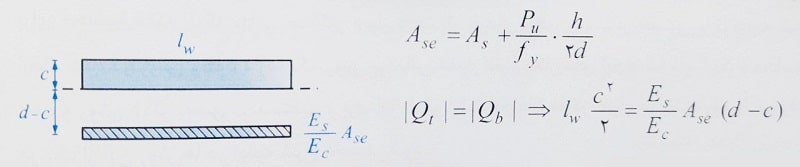
روش دوم: روش مستقیم
در این حالت، مقدار لنگر خمشی نهایی در وسط ارتفاع دیوار برابر است با:
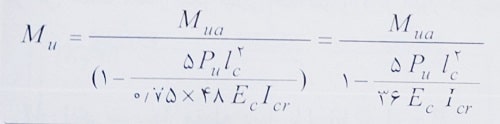
در این رابطه تعریف پارامترها مطابق حالت قبل می باشد.
مثال: در یک دیوار بتن آرمه با ضخامت 300 میلی متر، با لحاظ کردن اثر P-Δ، مقدار لنگر نهایی به اندازه 15 درصد بیشتر از حالتی بدست آمده که اثر P-Δ در نظر گرفته نشده است. چنانچه بار محوری نهایی این دیوار 20 درصد افزایش یابد، مقدار حداکثر لنگر نهایی دیوار با لحاظ کردن اثر P-Δ و با فرض ثابت باقی ماندن ممان اینرسی و لنگر خمشی اولیه مقطع در هر دو حالت، چگونه تغییر می کند؟ ( از روش مسنقیم استفاده شود).
1- در حدود 15 درصد افزایش می یابد. 2- در حدود 6 درصد افزایش می یابد.
3- در حدود 9.5 درصد افزایش می یابد. 4- در حدود 2.5 درصد افزایش می یابد.
حل: مطابق رابطه بالا داریم:
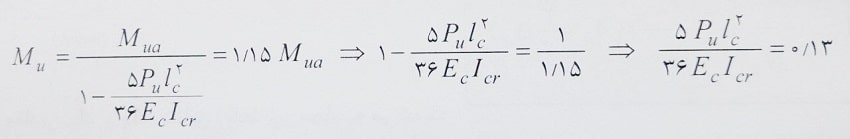
در ادامه با افزایش 20 درصدی بار محوری دیوار و با فرض ثابت ماندن سایر پارامترها، عبارت محاسبه شده 1.2 برابر شده و داریم:
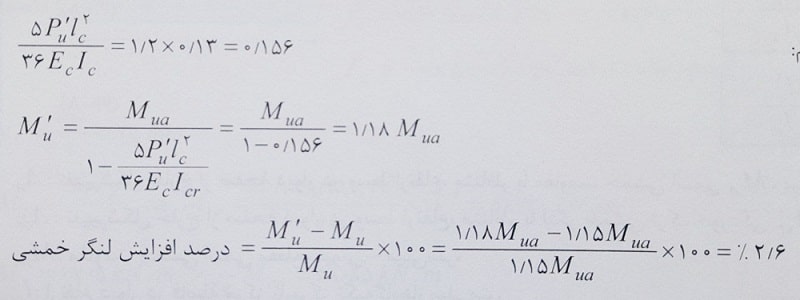
بنابراین گزینه 4 صحیح است.
تغییر شکل خارج از صفحه دیوار تحت بارهای بهره برداری در روش جایگزین
در بخش قبل حداکثر لنگر ضریبدار در وسط ارتفاع مقطع ناشی از اثرات P-Δ، در دیوار بدست آمده است. در این قسمت می خواهیم مقدار حداکثر تغییر مکان در مقطع وسط ارتفاع دیوار را تحت اثر بارهای بهره برداری (بارهای بدون ضریب) بدست آوریم. برای این منظور ابتدا مقدار لنگر خمشی حداکثر در مقطع وسط ارتفاع دیوار را تحت بارهای بهره برداری محوری و جانبی (شامل اثرات پی دلتا) به صورت زیر بدست آوریم:
![]()
Ma: حداکثر لنگر خمشی ناشی از بارهای بهره برداری، نیوتن – میلی متر.
Msa: حداکثر لنگر در دیوار در حالت بهره برداری بدون در نظر گرفتن اثرات P-Δ، نیوتن – میلی متر.
Ps: بار محوری بدون ضریب در وسط ارتفاع مقطع شامل وزن قطعه، نیوتن.
Δs: تغییر شکل خارج از صفحه دیوار ناشی از بارهای بهره برداری، میلی متر.
در این حالت با توجه به مقدار Ma بدست آمده، برای تعیین Δs با محاسبه مقدار لنگر ترک خوردگی دیوار Mcr از روابط زیر استفاده می شود:
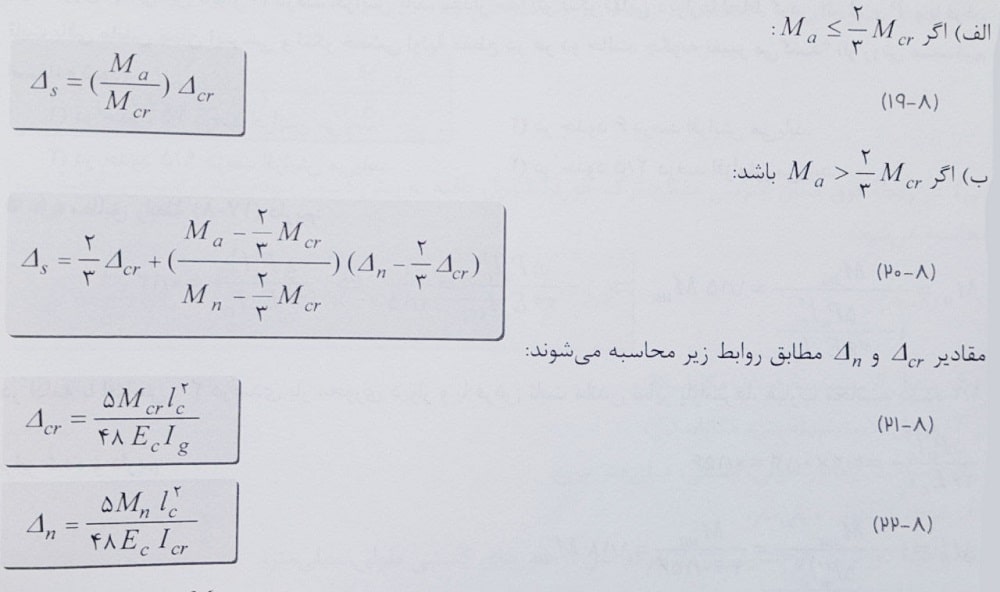
Δn: تغییر شکل خارج از صفحه دیوار در وسط ارتفاع، متناظر با مقاومت خمشی اسمی Mn میلی متر.
Δcr: تغییر شکل خارج از صفحه دیوار در وسط ارتفاع، متناظر با لنگر خمشی ترک خوردگی Mcr میلی متر.
Mn: مقاومت خمشی اسمی مقطع، نیوتن – میلی متر.
lc: ارتفاع دیوار در فاصله مرکز تا مرکز تکیه گاه- میلی متر.
در واقع در این روش به دلیل وابسته بودن مقادیر لنگر خمشی و تغییر مکان دیوار، روش حل به صورت یک روند تکراری خواهد بود. به این صورت که ابتدا با حدسیک تغییر شکل (پارامتر Δs) مقدار Ma تعیین شده، سپس با استفاده از مقدار بدست آمده برای لنگر Ma و مقایسه با لنگر ترک خوردگی Mcr، مجددا مقدار Δs محاسبه می شود.
در این شرایط مقدار بدست آمده برای Δs با مقدار فرض اولیه کنترل می گردد. در صورتی که این دو مقدار اختلاف محسوسی نداشته باشند، محاسبات نیازی به تکرار ندارد. اما چنانچه اختلاف اعداد زیاد باشد، مجددا لازم است مقدار فرض شده Δs اصلاح شده و محاسبات تا رسیدن به درصد خطای کم تکرار شود.
مثال: یک دیوار بتن آرمه به طول و ارتفاع 5 متر و ضخامت 150 میلی متر را در نظر بگیرید که تحت بارهای زنده و مرده با خروج از محوریت قرار گرفته است. با توجه به بارگذاری وارده مقادیر بار محوری مرده و زنده در وسط ارتفاع دیوار به ترتیب برابر 160 و 90 کیلو نیوتن و لنگر خمشی بهره برداری حداکثر در دیوار بدون لحاظ کردن اثر P-Δ برابر 60kn.m محاسبه شده است. در صورتی که در این دیوار از 25D16 به عنوان آرماتورهای قائم در یک شبکه و در وسط آن استفاده شده باشد، مقدار تغییر شکل خارج از صفحه دیوار تحت اثر بارهای برون محور را با لحاظ کردن اثرات لاغری تحت بارهای بهره برداری محاسبه کنید. بتن مصرفی از رده C25 و فولاد S400 می باشد. جرم مخصوص بتن 2300 کیلوگرم بر متر مکعب می باشد.
حل: با توجه به مواردی که گفتیم، ابتدا لنگر خمشی ناشی از حالت بهره برداری را تحت اثر لاغری با فرض Δs=30mm محاسبه می کنیم:
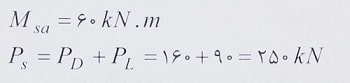
تذکر: دقت شود در محاسبه مقدار Ps، ضرایب ترکیب بار مطابق حالت بهره برداری و برابر 1 در نظر گرفته شده اند.
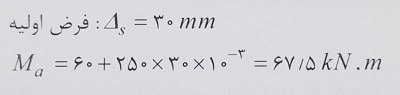
حال مقدار Ma بدست آمده را با مقدار 2/3Mcr مقایسه می کنیم. برای محاسبه Mcr، باید دقت شود که رفتار خارج از صفحه دیوار مد نظر بوده و در واقع خمش حول محور ضعیف انجام می شود. در این صورت با در نظر گرفتن پلان دیوار مطابق شکل زیر داریم:

برای محاسبه پارامتر Δs، باید ابتدا مقادیر Icr و Mcr محاسبه گردد. دقت شود در این حالت برای محاسبه لنگر خمشی اسمی مقاوم، مقطع دیوار دقیقا مطابق تیری به عرض 5 متر و ارتفاع 150 میلی متر در نظر گرفته شده و در این حالت ابتدا عمق بلوک فشاری محاسبه می شود:
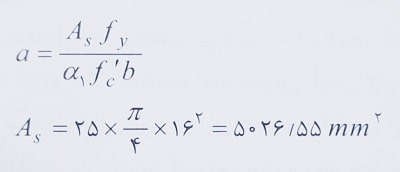
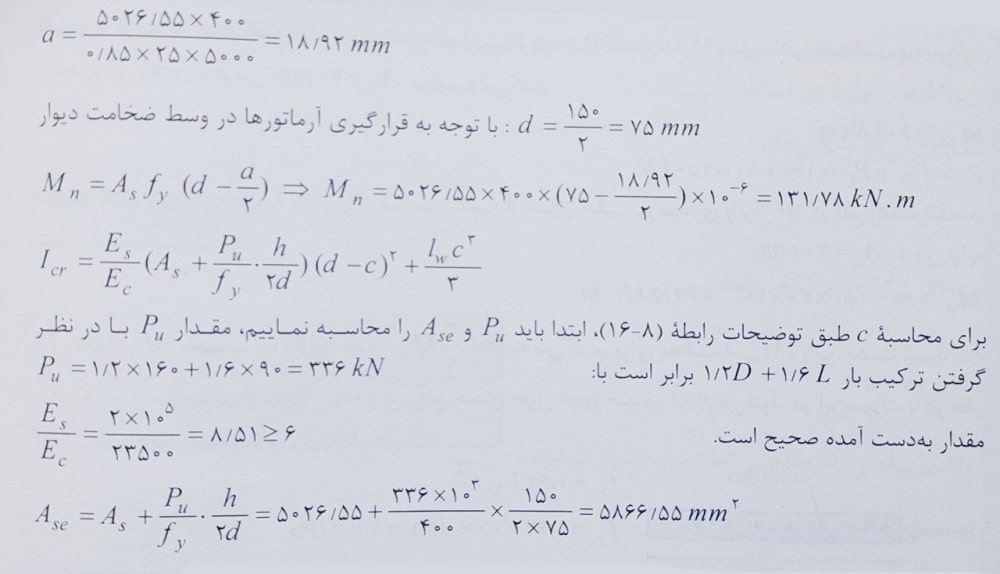

همانطور که مشاهده می شود، مقدار فرض اولیه برای Δs برابر 30 میلی متر بوده، در حالیکه این مقدار برابر 33 میلی متر بدست آمد. بنابراین فرض اولیه کمی خطا دارد و محاسبات برای رسیدن به دقت بیشتر باید مجددا تکرار نمود. در این خصوص با فرض اولیه 34 میلی متر با تقریب خوبی می توان به جواب رسید.
روش جایگزین برای طراحی دیوارهای لاغر – روش جایگزین برای طراحی دیوارهای لاغر – روش جایگزین برای طراحی دیوارهای لاغر


دیدگاه خود را ثبت کنید
تمایل دارید در گفتگوها شرکت کنید؟در گفتگو ها شرکت کنید.