تقریب نمودار اندرکنش به صورت دو خطی

یکی از روش های ساده سازی در تحلیل ستون هایی که تحت اندرکنش نیروی محوری و لنگر خمشی قرار دارند، تقریب نمودار اندرکنش به صورت دو خطی می باشد.

با توجه به اینکه تعیین معادله خط نسبت به منحنی بسیار ساده است، بنابراین با استفاده از تقریب نمودار اندرکنش، تحلیل مقطع در لحظه نهایی بسیار ساده تر خواهد بود. برای درک بهتر به شکل زیر که نمودار اندرکنش را به دو صورت دقیق و تقریبی نشان می دهد توجه کنید.

همانطور که در شکل مشاهده می کنید با استفاده از این تقریب، در واقع ناحیه امن داخل نمودار اندرکنش کوچکتر شده و مقادیر نیروی محوری و لنگر خمشی نظیر حالت نهایی مقطع، کمی تفاوت با مقدار واقعی دارند.

بر این اساس معادله خط ها در دو ناحیه قبل از رسیدن به نقطه بالانس (ناحیه AB) و پس از آن (BC) به صورت زیر بدست می آید:

نمودار اندرکنش تحت نیروی کششی و لنگر خمشی

در بخش های قبل مواردی را بررسی کردیم که نیروی محوری وارد بر ستون از نوع فشار بود. دراین قسمت می خواهیم در مورد منحنی اندرکنش در زیر محور افقی، یعنی هنگامی که نیروی کششی به تسون اعمال می شود بحث کنیم.

منحنی اندرکنش در ناحیه کششی را نیز می توان با تقریب خوبی با یک خط مطابق آنچه در شکل زیر مشخص شده است بازنویسی کرد. در این صورت معادله این خط برابر است با:

T_n: مقاومت کششی ستون

M_n: لنگر خمشی همزمان با مقاومت کششی T_n

P_nt,max: حداکثر مقاومت کششی محوری اسمی ستون

M₀: لنگر خمشی خالص اسمی ستون.

مثال: منحنی اندرکنش نیروی محوری – لنگر خمشی در یک ستون بتن آرمه با مقطع مستطیلی به شکل زیر نشان داده شده است. در مورد وضعیت گسیختگی مقطع در هر یک از سوالات زیر اظهار نظر کنید. در هر دو حالت ضریب φ=0.9 فرض می شود.

الف)هنگامی که نیروی محوری فشاری 1800 kN و لنگر خمشی 400 kN.m بر مقطع اعمال می شود.

ب)هنگامی که نیروی محوری کششی 900 kN و لنگر خمشی 90 kN.m بر مقطع اعمال می شود.

حل:

الف) برای حل این سوال ابتدا با توجه به مقادیر نیرو و لنگر خمشی داده شده، موقعیت نیروی محوری را بر روی نمودار پیدا می کنیم. همانطور که مشاهده می شود، نیروی محوری فشاری اسمی 2000 kN پایین تر از نقطه بالانس قرار گرفته است.

با توجه به این نکته معادله خط ناحیه مورد نظر بدست آورده سپس مقدار نیروی محوری را در معادله جایگزین کرده و لنگر خمشی نظیر را محاسبه می کنیم:

با محاسبه M_n و مقایسه آن با لنگر خمشی اعمالی به ستون، سه حالت زیر اتفاق می افتد:

بنابراین ستون تحت ترکیب نیرو و لنگر خمشی داده شده گسیخته نمی شود.

مثال: منحنی اندرکنش فشار و خمش برای یک ستون کوتاه بتنی با تنگ بسته مطابق شکل مقابل داده شده است. حداکثر مقاومت اسمی فشاری محوری مقطع به کدامیک از مقادیر زیر نزدیکتر است؟

1)800 کیلونیوتن

2)1000 کیلونیوتن

3)1200 کیلونیوتن

4)400 کیلونیوتن

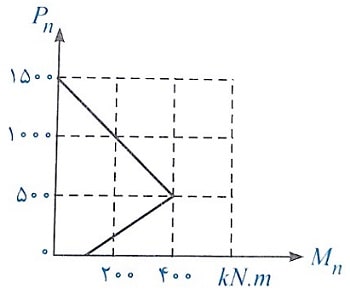
حل: با توجه به نمودار داده شده مقدار P₀=1500 kN می باشد، با توجه به این که در ستون از تنگ بسته استفاده شده است، بنابراین حداکثر مقاومت فشاری محوری اسمی آن برابر است با: